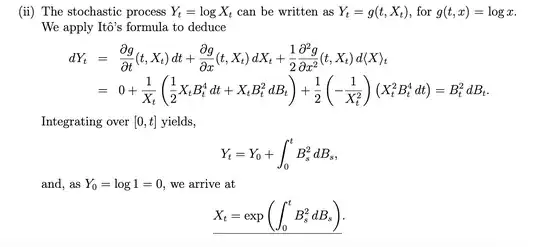The function $g$ depends only on $X_t$, we have :
\begin{equation}
\begin{split}
dg(X_t) &= \partial_x g(X_t)dX_t + \frac{1}{2}\partial_x^2g(X_t))dt \\
dY_t &= \frac{1}{X_t}(\frac{1}{2} X_t B_t^4dt + X_t B_t^2 dB_t) -\frac{1}{2} \frac{1}{X_t^2}d\langle X\rangle_t \\
\end{split}
\end{equation}
Since $$dX_t = \underbrace{\frac{1}{2} X_t B_t^4}_{b(X_t)}dt + \underbrace{X_t B_t^2}_{\sigma(X_t)}dB_t$$
then $d\langle X \rangle_t$ is given by :
$$\implies d\langle X\rangle_t = \sigma^2(X_t)dt=(X_tB_t^2)^2dt=X_t^2B_t^4dt$$
You get
$$dY_t=B_t^2dB_t\implies Y_t=\underbrace{Y_0}_{=0}+\int_0^tB_s^2dB_s=\int_0^tB_s^2dB_s$$
Finally,
$$X_t=\exp\left(\int_0^tB_s^2dB_s\right)$$
Note : Itô processes of the form
$$X_t=X_0+\int_0^t b(s,X_s)ds+\int_0^t \sigma(s,X_s)dB_s$$
have the quadratic variation
$$\langle X\rangle_t=\int_0^t \sigma^2(s,X_s)ds$$
For a detailed proof on why it is equal to the previous quantity, check this answer here.
EDIT
A quick explanation on why $dB^2_t=d\langle B\rangle_t = dt$:
Since $$B_t=\int_0^tdB_s=\int_0^t \textbf{1}\times dB_s\implies \langle B\rangle_t=\int_0^t \textbf{1}^2 ds=t \implies d\langle B\rangle_t = dt$$
As for your formula : Suppose $X_t=X_0+\int_0^t b(s,X_s)ds +\int_0^t \sigma(s,X_s)dB_s$. Then for any twice-differentiable scalar function $g$ :
\begin{equation}
\begin{split}
dg(t,X_t)&=\frac{\partial g}{\partial t}(t,X_t)dt+\frac{\partial g}{\partial x}(t,X_t)dX_t+\frac{1}{2}\frac{\partial^2 g}{\partial^2 t}(t,X_t)d\langle X \rangle_t\\
&=\frac{\partial g}{\partial t}(t,X_t)dt+\frac{\partial g}{\partial x}(t,X_t)\left(b(t,X_t)dt + \sigma(t,X_t)dB_t\right)+\frac{1}{2}\frac{\partial^2 g}{\partial^2 x}(t,X_t)(\sigma^2(t,X_t)dt)\\
&=\left(\frac{\partial g}{\partial t}(t,X_t)+ b(t,X_t)\frac{\partial g}{\partial x}(t,X_t)+\frac{1}{2}\frac{\partial^2 g}{\partial^2 x}(t,X_t)\sigma^2(t,X_t)\right)dt\\
&+\left( \sigma(t,X_t)\frac{\partial g}{\partial x}(t,X_t) \right)dB_t
\end{split}
\end{equation}
I guess you can see the term you missed out.
Hope this explains your questions.