Let's consider a bit more general case
$$I(x,a)=\int_0^1\cos(xt^a)\tan tdt=\Re\int_0^1e^{ixt^a}\tan tdt\overset{xt^a=z}{=}\frac{1}{ax^{1/a}}\Re\int_0^xe^{iz}\tan\left(\frac{z}{x}\right)^\frac1az^{\frac1a-1}dz$$
Decomposing $\tan$ into the series
$$=\frac{1}{ax^{1/a}}\Re\int_0^xe^{iz}\left(\big(\frac{z}{x}\big)^{1/a}+\frac{1}{3}\big(\frac{z}{x}\big)^{3/a}+...\right)z^{\frac 1a-1}dz\tag{1}$$
Let's consider the first term:
$$I_1=\frac{1}{ax^{1/a}}\Re\int_0^xe^{iz}\Big(\frac{z}{x}\Big)^{1/a}z^{\frac 1a-1}dz=\frac{1}{ax^{2/a}}\Re\int_0^xe^{iz}z^{\frac2a-1}dz\tag{2}$$
Next, we integrate along a quarter-circle in the complex plane: $0\to x\to ix\to i0$, adding the arch of radius $x$. We do not have poles inside our contour; therefore,
$$\oint_C=0\,\Rightarrow\,I_1+\frac{1}{ax^{2/a}}\Re\,e^{\frac{\pi i}{a}}\int_x^0e^{-z}z^{\frac2a-1}dz+I_{C_x}=0$$
where $I_{C_x}$ is the integral along the arch of the radius $x$.
Extending integration of the second term to $\infty$ (and, therefore, dropping exponentially small corrections),
$$I_1\sim\frac{\cos\frac{\pi}{a}\Gamma\left(\frac2a\right)}{ax^{2/a}}-I_{C_x}$$
To estimate $I_{C_x}$, we use the Jordan' lemma. Using $\sin\phi>\frac2\pi\phi$ for $\phi\in[0;\frac\pi2]$,
$$|I_{C_x}|=\frac{1}{ax^{2/a}}\left|\int_0^{\pi/2}e^{ix\cos\phi-x\sin\phi}x^\frac2ae^{i\phi\frac2a}id\phi\right|<\frac{1}{a}\int_0^{\pi/2}e^{-\frac2\pi x\phi}d\phi<\frac{\pi}{2ax}$$
We see that $|I_{C_x}|\ll I_1$ at $x\to\infty$ and can be dropped , if $x^\frac2a\ll x$, or $\,\boxed{a>2}$.
In the same way we can evaluate next terms of $\tan$ decomposition and get, for example,
$$I(x,a)=\int_0^1\cos(xt^a)\tan tdt\sim\frac{\cos\frac{\pi}{a}\Gamma\left(\frac2a\right)}{a\,x^{2/a}}+\frac{\cos\frac{2\pi}{a}\Gamma\left(\frac4a\right)}{3a\,x^{4/a}},\,\,a>4\tag{3}$$
For $a=3$ we are only allowed to keep the first term:
$$\int^1_0 \cos(xt^3)\tan(t)dt\sim\frac{\cos\frac{\pi}{3}\Gamma\left(\frac23\right)}{3x^{2/3}}=\frac16\Gamma\big(\frac23\big)\,x^{-\frac23}\tag{4}$$
$\bf{Explicite \,form \,of\, full \,asymptotic}$
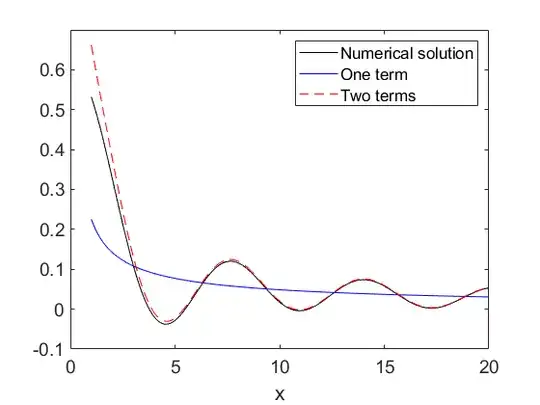
In his post @AxelT evaluated first oscillating asymptotic term, which gives very good approximation even at $x\sim1$. It would be also interesting to get full asymptotic.
Using integration in the complex plane, we got above
$$I(x,a)=\frac{1}{ax^{1/a}}\Re\int_0^xe^{iz}\tan\left(\frac{z}{x}\right)^\frac1az^{\frac1a-1}dz=\frac{1}{ax^{1/a}}\Re \,e^\frac{\pi i}{2a}\int_0^xe^{-z}\tan\left(\frac{z^\frac1a}{x^\frac1a}e^\frac{\pi i}{2a}\right)z^{\frac1a-1}dz$$
$$-\,I_{C_x}\tag{5}$$
where $I_{C_x}$ is the integral along the arch of the radius $x$:
$$I_{C_x}=\frac{1}{ax^{1/a}}\Re\int_0^{\pi/2}e^{ixe^{i\phi}}e^{\frac{i\phi}{a}}\tan\big(e^{\frac{i\phi}{a}}\big)x^\frac1ae^{i\phi}id\phi\overset{s=e^{i\phi}}{=}\frac1a\int_1^{e^{\frac{\pi i}{2}}}e^{ixs}\tan(s^\frac1a)s^\frac1ads\tag{6}$$
Integrating (6) several times by part and dropping exponentially small terms ($\sim e^{-\frac{\pi x}{2}}$)
$$I_{C_x}\sim\frac{1}{a}\Re\left(-\frac{e^{ix}}{ix}f^{(0)}(s,a)|_{s=1}+\frac{e^{ix}}{(ix)^2}f^{(1)}(s,a)|_{s=1}-\frac{e^{ix}}{(ix)^3}f^{(2)}(s,a)|_{s=1}-...\right)$$
where we denoted
$$f^{(k)}(s,a)|_{s=1}:=\frac{\partial^k}{\partial s^k}s^\frac1a\tan(s^\frac1a)\Big|_{s=1}$$
Rearranging
$$-I_{C_x}\sim\frac{\sin x}{ax}\left(f^{(0)}(s,a)-\frac{f^{(2)}(s,a)}{x^2}+...\right)\bigg|_{s=1}+\frac{\cos x}{ax^2}\left(f^{(1)}(s,a)-\frac{f^{(3)}(s,a)}{x^2}+...\right)\bigg|_{s=1}$$
$$=\frac1a\sum_{n=1}^\infty\frac{\sin\big(\frac{\pi(n-1)}{2}+x\big)}{x^n}\left(s^\frac1a\tan s^\frac1a\right)^{(n-1)}\,\bigg|_{s=1}\tag{7}$$
Using the series of $\tan$
$$\tan t=\sum_{n=1}^\infty(-1)^{n-1}\frac{4^n(4^n-1)}{(2n)!}B_{2n}t^{2n-1}$$
and integrating term by term (extending integration to $\infty$)
$$\frac{1}{ax^{1/a}}\Re \,e^\frac{\pi i}{2a}\int_0^xe^{-z}\tan\left(\frac{z^\frac1a}{x^\frac1a}e^\frac{\pi i}{2a}\right)z^{\frac1a-1}dz\sim\frac1a\sum_{n=1}^\infty\frac{(-1)^{n-1}4^n(4^n-1)B_{2n}}{(2n)!}\frac{\cos\frac{\pi n}{a}\Gamma\big(\frac{2n}{a}\big)}{x^\frac{2n}{a}}\tag{8}$$
Putting (7) and (8) into (5), we get the desired asymptotics:
$$\color{blue}{I(x,a)\sim\frac1a\sum_{n=1}^\infty\frac{(-1)^{n-1}4^n(4^n-1)B_{2n}}{(2n)!}\frac{\cos\frac{\pi n}{a}\Gamma\big(\frac{2n}{a}\big)}{x^\frac{2n}{a}}}$$
$$\color{blue}{+\,\frac1a\sum_{n=1}^\infty\frac{\sin\big(\frac{\pi(n-1)}{2}+x\big)}{x^n}\left(s^\frac1a\tan s^\frac1a\right)^{(n-1)}\,\bigg|_{s=1}}$$
Here we have the only limitation $\color{blue}{a>0}$.
If we want to take several first terms, the solution - the sequence of the terms we have to keep - depends, of course, on $a$. For example, for $a=3$ we get the series
$$I(x,3)\sim\frac{\cos\frac\pi3\Gamma\big(\frac23\big)}{3x^\frac23}+\frac{\sin x\tan1}{3x}+\frac{\cos\frac{2\pi}{3}\Gamma\big(\frac43\big)}{9x^\frac43}+\frac{2\cos\pi\,\Gamma(2)}{45x^2}+\frac{\cos x}{9x^2}\left(\tan1+\frac{1}{\cos^21}\right)$$
$$+\,O\left(\frac1{x^\frac83}\right)$$