For two ellipses with given semi-major and semi-minor axes, and orientations with respect to the $x$ and $y$ axes. Fix the center of one ellipse, then you can find the locus of the center of the second ellipse when its tangent to the first fixed ellipse.
Let the two ellipses be modelled by
$ (r - r_1)^T Q_1 (r - r_1) = 1 $
$ (r - r_2)^T Q_2 (r - r_2) = 1 $
Select the tangency points $T$ on the first ellipse, then the normal vector extending out of the first ellipse is along the vector
$ g_1 = Q_1 (T - r_1) $
We want this normal to be parallel to the gradient of the second ellipse, which is given by
$ g_2 = Q_2 (T - r_2 )$
So now we have
$ Q_2 (T - r_2) = K Q_1 (T - r_1) $
For some $K \lt 0 $
From the last equation, we get
$ T - r_2 = K Q_2^{-1} Q_1 (T - r_1 ) $
Since $T$ is on the second ellipse, then
$ (T - r_2)^T Q_2 (T - r_2) = 1 $
Therefore,
$ K^2 (T - r_1) Q_1 Q_2^{-1} Q_1 (T - r_1 ) = 1 $
And this gives the value of $K$ (remember $K$ is negative).
Having found the proportionality constant $K$, we go back to the previous equation and solve for $r_2$
The previous equation is
$ T - r_2 = K Q_2^{-1} Q_1 (T - r_1 ) $
From which,
$ r_2 = T - K Q_2^{-1} Q_1 (T - r_1 ) $
Changing $T$ over all the perimeter of the first ellipse generates the locus of $r_2$. This is illustrated in the following GIF image
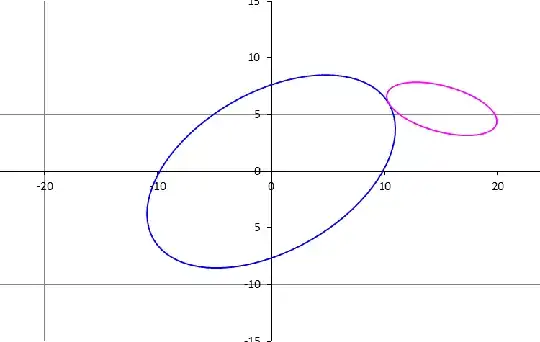
The code (VBA for MS-Excel) that I used to generate the GIF image is included below
Public Sub tangent_ellipse_to_another_ellipse()
Dim q1(2, 2), q2(2, 2), q2inv(2, 2) As Double
Dim d1(2, 2), d2(2, 2), r1(2, 2), r2(2, 2), r1t(2, 2), r2t(2, 2) As
Double
Dim d1p(2, 2), d2p(2, 2) As Double
Dim pts(91, 2) As Double
Dim th1 As Double, th2 As Double
Dim k1 As Double
Dim rc1(2), rc2(2), rt(2) As Double
Dim v1(2, 2), v2(2, 2) As Double
th1 = p / 6
th2 = -p / 12
d1(1, 1) = 1 / 12 ^ 2
d1(2, 2) = 1 / 7 ^ 2
d2(1, 1) = 1 / 5 ^ 2
d2(2, 2) = 1 / 2 ^ 2
For i = 1 To 2
d1p(i, i) = 1 / Sqr(d1(i, i))
d2p(i, i) = 1 / Sqr(d2(i, i))
Next i
r1(1, 1) = Cos(th1)
r1(2, 2) = Cos(th1)
r1(2, 1) = Sin(th1)
r1(1, 2) = -Sin(th1)
Call multiply(2, 2, 2, r1, d1p, v1)
Call transpose(2, 2, r1, r1t)
Call multiply(2, 2, 2, r1, d1, q1)
Call multiply(2, 2, 2, q1, r1t, q1)
r2(1, 1) = Cos(th2)
r2(2, 2) = Cos(th2)
r2(2, 1) = Sin(th2)
r2(1, 2) = -Sin(th2)
Call multiply(2, 2, 2, r2, d2p, v2)
Call transpose(2, 2, r2, r2t)
Call multiply(2, 2, 2, r2, d2, q2)
Call multiply(2, 2, 2, q2, r2t, q2)
Call invert(q2, 2, q2inv, ierr)
For ipass = 1 To 2
For i1 = 0 To 90
k = 1
narcs = 0
t = 4 * i1 * p / 180
u1(1) = Cos(t)
u1(2) = Sin(t)
Call multiplyv(2, 2, v1, u1, u2)
Call vadd(2, rc1, u2, rt)
Call multiplyv(2, 2, q1, u2, u3)
k1 = -1 / Sqr(xtqy(2, q2inv, u3, u3))
Call multiplyv(2, 2, q2inv, u3, u4)
Call vscale(2, u4, k1, u4)
For i = 1 To 2
rc2(i) = rt(i) - u4(i)
pts(i1 + 1, i) = rc2(i)
Next i
Call draw_ellipse(rc1, v1, 5)
Call draw_ellipse(rc2, v2, 7)
Call draw_points(1, i1 + 1, pts, 8)
If ipass = 2 Then Call plot_curve(0, 1, 2, 0, 1, "c:\gifs",
"tan_ell" + LTrim(Str(i1)))
Next i1
Next ipass
End Sub
The problem as it posed in the question, is somewhat different from what I've presented above, namely, we are given the first ellipse whose equation is
$ (r - r_1)^T Q_1 (r - r_1) = 1 $
where $Q_1$ and the center $r_1$ are known. In addition, we have the second ellipse equation,
$ (r - r_2)^T Q_2 (r - r_2) = 1 $
where $Q_2$ is known, but $r_2$ is partially known. In the question, we have
$ Q_1 = \begin{bmatrix} \dfrac{1}{50^2} && 0 \\ 0 && \dfrac{1}{25^2} \end{bmatrix} $
$ r_1 = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $
$Q_2 = \begin{bmatrix} \dfrac{1}{20^2} && 0 \\ 0 && \dfrac{1}{50^2} \end{bmatrix} $
And
$ r_2 = \begin{bmatrix} - 35 \\ y_2 \end{bmatrix} $
We want to determine the tangency between the first and second ellipses. For this purpose let the tangency point be
$ T = \begin{bmatrix} x \\ y \end{bmatrix} $
Then we have $T$ on both ellipses, i.e.
$ (T - r_1)^T Q_1 (T - r_1) = 1 $
and
$ (T - r_2)^T Q_2 (T - r_2) = 1 $
The first equation expands as follows
$ T^T Q_1 T + r_1^T Q_1 r_1 - 2 T^T Q_1 r_1 = 1 $
And the second equation expands as follows
$ T^T Q_1 T + r_2^T Q_1 r_2 - 2 T^T Q_1 r_2 = 1 $
Note here that $r_2$ is not a constant vector.
The third equation that we need is the tangency equation, we as discussed above is
$ Q_2 (T - r_2) = K Q_1 (T - r_1) $
This introduces a fourth unkown which is the parameter $K$, but this can be eliminated by dividing the two components of the above vector equation, and after cross multiplication this result in
$ \left( Q_{2_{11}} (x + 35) + Q_{2_{12}} (y - y_2) \right) \left( Q_{1_{21}} (x - r_{1x}) + Q_{1_{22}} (y - r_{1y} \right) = \left( Q_{2_{21}} (x + 35) + Q_{2_{22}} (y - y_2) \right) \left( Q_{1_{11}} (x - r_{1x} ) + Q_{1_{12}} (y - r_{1y} ) \right) $
In the question, the off-diagonal elements of $Q_1$ and $Q_2$ are zero, so this equation simplifies to
$ \left( Q_{2_{11}} (x + 35) \right) \left( Q_{1_{22}} (y - r_{1y} \right) = \left( Q_{2_{22}} (y - y_2) \right) \left( Q_{1_{11}} (x - r_{1x} ) \right) $
We now have three quadratic equations in the three unknowns $x, y, y_2$, and they can be solved using a math software application such as Mathematica, or online at www.wolframalpha.com
I found six valid solutions to this problem.
There are listed below:
- $ T = (-31.75477, -19.31083) , y_2 = -68.64823 $
- $ T = (-31.75477, 19.31083) , y_2 = 68.64823 $
- $T = (-40.23178, -14.84422) , y_2 = 33.41474 $
- $T= (-40.23178, 14.84422), y_2 = -33.41474 $
- $T = (-48.98703, -5.00675) , y_2 = 30.73213 $
- $T = (-48.98703, 5.00675), y_2 = -30.73213 $
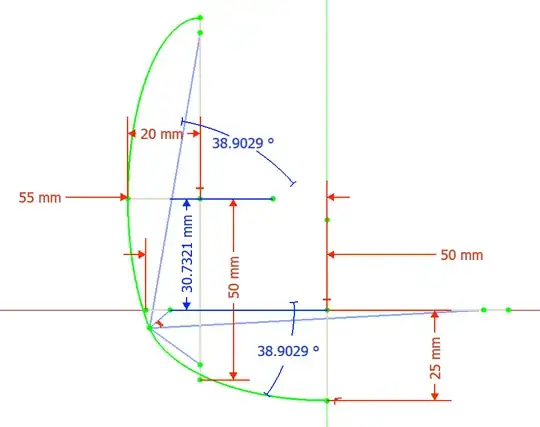 Angles are badly displayed but are bound to the respective lines between the tangency point and the foci
Angles are badly displayed but are bound to the respective lines between the tangency point and the foci