Consider the expression $$ f(\mathbf{x},n)=\sum_{k=0}^{n} \frac{e^{-k^2\overline{x_k}}-e^{-(k+1)^2\overline{x_k}}}{(2k+1)\overline{x_k}} $$ where $\mathbf{x}=[x_{-n},\cdots,x_{-2},x_{-1},x_0,x_1,x_2,\cdots,x_{n}]^T$ and $$ \overline{x_k}=\frac{1}{2k+1}\sum_{|i|\leq k} x_i $$ with $0<x_i<\infty$, for all $i\in\{-n,...,-1,0,1,...,n\}$.
What is $\lim_{n\to\infty}f(\mathbf{x},n)$? If not a closed formula, is it possible to find an upper bound?
My attempt: Following @metamorphy's answer presented here, for the case where $x_i\equiv x,\forall i$, and given that $\{x_i\}$ is bounded, one would hope there exists $k^*$ such that $$ f(\mathbf{x},\infty)=\sum_{k=0}^{\infty} \frac{e^{-k^2\overline{x_k}}-e^{-(k+1)^2\overline{x_k}}}{(2k+1)\overline{x_k}}\simeq \frac{1}{\overline{x_{k^*}}} \sum_{k=0}^{\infty} \frac{e^{-k^2\overline{x_{k^*}}}-e^{-(k+1)^2\overline{x_{k^*}}}}{2k+1} $$ which, following the answer to the linked question, leads to the local approximation $$ f(\mathbf{x},\infty)\simeq \frac12\sqrt{\frac{\pi}{\overline{x_{k^*}}}} $$ However, in simulations, this does not seem to work for numerical attempts on various values of $k^*$. Nonetheless, I expect an approximation like this to be possible.
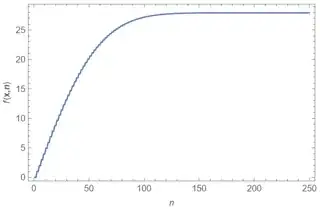
Just to better visualize the problem, here is the plot of $f(\mathbf{x},n)$, where the "data" vector $\mathbf{x}$ was generated via a random walk with very small increments ($10^{-5}$) and $x_i\in(0,0.1)$
The goal is to approximate the blue curve. Any ideas?
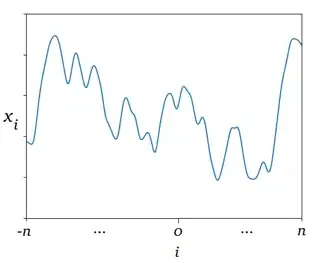
Comment on $\mathbf{x}$: The randomness of $\mathbf{x}$ might difficult finding a potential solution and make this problem way too broad. Therefore, we may take it to behave "continuously" enough. For example, it can be taken to be a fine discretisation of a continuous function, as sketched here
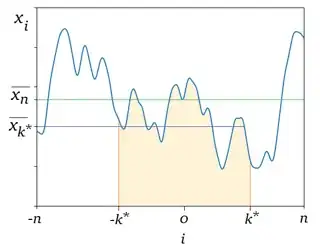
Naturally the answer should be $\mathbf{x}$-dependent, but I wonder if it is possible to still make an assertion on an approximation to $f$, given, for example, a local mean approximation, as seen, for some $k^*$,
Where $\overline{x_n}$ is the overall mean. Note that, for each $k$, the mean changes little, and we may also assume $$ |\overline{x_k}-\overline{x_{k-1}}|<\epsilon $$ for some small $\epsilon$.