solution verification for a proof of "the magic diagram"

Question

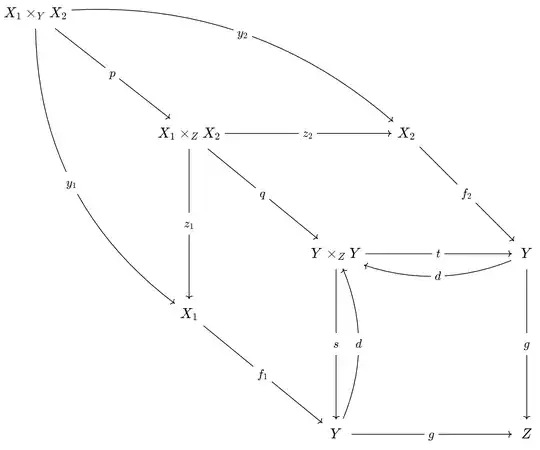
There are already many threads about this result, like The "magic diagram" is cartesian, i.e, the following diagram is a pullback:

$$ \require{AMScd} \begin{CD} X_1\times_Y X_2 @>{p}>> X_1\times_Z X_2\\ @V{h=f_1\circ y_1=f_2\circ y_2}V V @V{q}V V\\ Y @>{d}>> Y \times_Z Y \end{CD} $$

Using the notation from the following diagram

for some subtleness in the diagram (mainly, some part of it does not commute). I am asking for some help on verifying this proof, to see if I missed any thing:

Denote $h = f_1 \circ y_1 = f_2 \circ y_2$. Then $d \circ h = q \circ p$ for

• $s \circ d \circ h = h = f_1 \circ y_1 = f_1 \circ z_1 \circ p = s \circ q \circ p$
• $t \circ d \circ h = h = f_2 \circ y_2 = f_2 \circ z_2 \circ p = t \circ q \circ p$ Both two equalities use $s\circ d = 1$ and $t \circ d = 1$.

Then by the universal property for $Y \times_Z Y$, one has $d \circ h = q \circ p$, i.e, the cartesian diagram commutes.

Given $i: W \to Y$ and $j: W \to X_1 \times_Z X_2$ with $d \circ i = q \circ j$, one has $f_1 \circ z_1 \circ j = s \circ q \circ j = s \circ d \circ i =i$ and $f_2 \circ z_2 \circ j = t \circ q\circ j = t \circ d \circ i = i$. Hence by the universal property of $X_1 \times_Y X_2$, there exists an unique morphism $l: W \to X_1 \times_Y X_2$ such that $y_1 \circ l = z_1 \circ j$ and $y_2 \circ l = z_2 \circ j$. Since $y_1 = z_1 \circ p$ and $y_2 = z_2 \circ p$, one has $z_1 \circ p \circ l = z_1 \circ j$ and $z_2 \circ p \circ l = z_2 \circ j$. Hence $j = p \circ l$ by the universal property of $X_1 \times_Z X_2$. And $i = s \circ d \circ i = s \circ q \circ j = s \circ q \circ p \circ l = f_1 \circ y_1 \circ l = h \circ l$. (From here, one has $j = p \circ l$ implying $i = h \circ l$.) Hence the cone $\{i: W \to Y$, $j: W \to X_1 \times_Z X_2\}$ factors through $X_1 \times_Y X_2$ via $l$.

If it factors through some other $l': W \to X_1 \times_Y X_2$, i.e., $j = p \circ l'$ (and hence $i = s \circ d \circ i = s \circ q \circ j = s \circ q \circ p \circ l' = h \circ l'$). Then $y_1 \circ l' = z_1 \circ p \circ l' = z_1 \circ j$ and $y_2 \circ l' = z_2 \circ p \circ l' = z_2 \circ j$. By the universal property for $l$, one has $l' = l$. $\square$

Is it correct? Am I missing something? Mainly I am considering three points:

1. It seems condition for factoring through the magic diagram only need "a half" (and the other half can be obtained from it)?
2. The diagram used in proof seems awkward: $f_1 \circ y_1 = f_2 \circ y_2$ is not shown in it, and $d\circ s$, $d \circ t$ is not the idenity map for $Y \times_Z Y$. Is there any other uncommute path in it I used? Is it a better layout for the diagram that any path with same begin and ending commute?

Thank you in advance.