I am looking for a parametric closed curve that roughly resembles a bean.
I am looking for something with an explicit parametrization of the form $C(t) = (X(t), Y(t))$
I tried searching online but "parametric bean" is not yielding much of use.
I am looking for a parametric closed curve that roughly resembles a bean.
I am looking for something with an explicit parametrization of the form $C(t) = (X(t), Y(t))$
I tried searching online but "parametric bean" is not yielding much of use.
A bit of experimentation got me to this:
It has the formula $$(\cos(t)-\frac{0.6}{1+9t^2},\sin(t))$$
Taken over the interval $[-\pi,\pi]$.
It has the disadvantage of not being periodic, but I don't know if that's a requirement, and it should be a relatively easy fix. It's also not easy to work with analytically, but I don't know what you're planning to do with it, so I don't know if that's important.
If you want it more curved you can go with: $$(\cos(t)-\frac{1}{1+4t^2},\sin(t))$$
HINT:
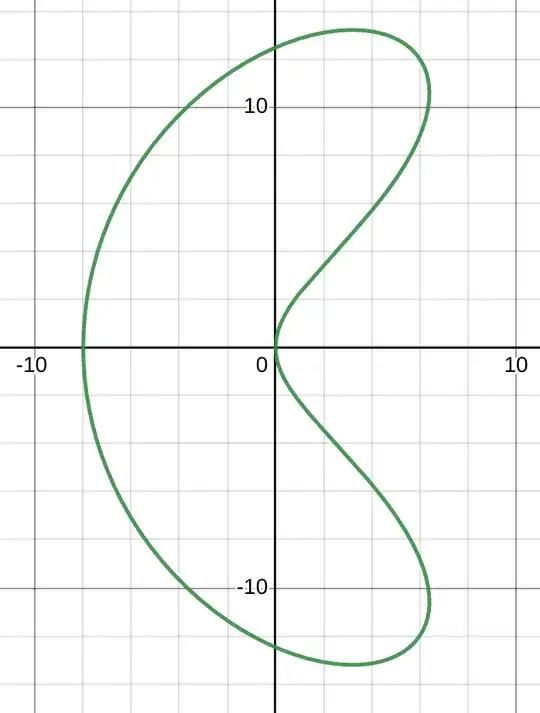
The domain inside is equivalent to the inside of a disk ( Riemann theorem)-- so try using a conformal map. Take a disk centered at the origin, dilate on the vertical and shift to the right. Now apply the complex map $z \mapsto z^2$, (even $z\mapsto z^n$). Because the square map doubles the argument the tall straight bean will wrap around the origin. Example:
$$t \mapsto (x^2-y^2, 2 x y)$$ where $(x,y)= (2 + \cos t , 3 \sin t)$ gets us a cashew nut.
$\bf{Added:}$ Should we want a filliform shape, like a snake, consider its spine ( a curve ), write as is the image of $P(t)$ over a segment ( $P$ analytic), then extend $P$ around the segment and consider the image of a flat ellipse approximating the segment).
$\bf{Added:}$ We can also do surfaces in $3D$, by deforming some ellipsoids. Here is an example of a surface, image of an ellipsoid under inversion. (Looks like a cashew nut, in 3D).
Here is a simple approach using connected circular arcs with (set apart parameter $t$ which is implicit), uses two parameters $a,b$ (which are the circles radii). For an interactive experience, move the sliders $a,b$ in this Geogebra animation here ; click on the "algebra" icon on the left if you want to see details.
The circular arcs are $P'P$ centered in $O$, $PR$ centered in $Q$, $RR'$ centered again in $O$, $R'P'$ centered in $Q'$.
Please note that any connecting point of two circular arcs is aligned with the centers of these arcs, warranting "smoothness" (differentiability) at the connecting point.
This interesting question about curve synthesis made me de-lurk. Here's my modest attempt:
$$\begin{align*}x&=3+2\sin t+\cos 2t\\y&=4\cos t-\sin 2t\end{align*}\quad t\in[0,2\pi]$$
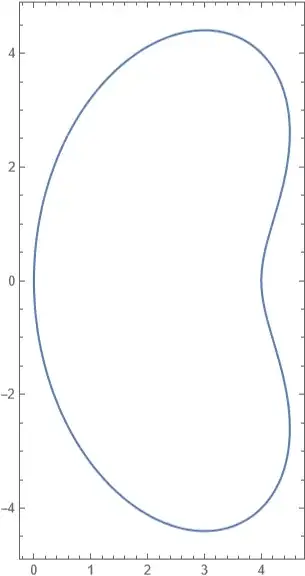
I don't want to say too much about where it came from, except that it was part of a series of experiments on fudging around with hypotrochoids.