Ring of fractions of $\Bbb Z/9\Bbb Z$

Question

I am trying to understand ring of fractions and I have this question: From ring $\Bbb Z/9\Bbb Z$ determine the different rings of fractions that can be obtained according to the choice of $D$.

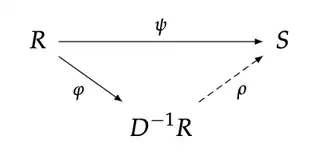
Dummit 7.5: Theorem 15. Let $R$ be a commutative ring. Let $D$ be any nonempty subset of $R$ that does not contain $0$, does not contain any zero divisors and is closed under multiplication. Then there is a commutative ring $Q$ with $1$ such that $Q$ contains $R$ as a subring and every element of $D$ is a unit in $Q$. (The ring $Q$ is called the ring of fractions of $D$ with respect to $R$ and is denoted $D^{-1}R$.)

So, the first thing I did was to find the subset $D$. I consider there are four subsets with this characteristics: $D_1 =$ {1}, $D_2 =$ {1, 8}, $D_3 =$ {1, 4, 7}, $D_4 =$ {1, 2, 4, 5, 7, 8}. Then, I wrote the elements of $D_1^{-1}R$, nine elements, so I claim is isomorphic to $\Bbb Z/9\Bbb Z$. The same way, $D_2^{-1}R$, nine different elements again and this ring would be isomorphic to $\Bbb Z/9\Bbb Z$.

I am not quite sure of my procedure, feels like I'm doing something wrong. I would really appreciate your help to guide me on the right way, or any advice to find those different ring of fractions.

Answer 1

To form the ring of fractions of a commutative ring, you use its set of regular elements $S$.

We always have the image of $R$ in $RS^{-1}$, the elements of the form $r/1$.

For each unit $u\in R\subseteq S$, consider an element like $r/u\in RS^{-1}$. Using definitions it's easy to verify that $r/u= ru^{-1}/1$, and since $ru^{-1}\in R$ we see that every fraction of the form $r/u$ is nothing new, it's just something in (the image of) $R$.

So for a commutative ring whose regular elements are exactly the units, localization doesn't produce anything new.

This includes not only rings like $\mathbb Z/n\mathbb Z$ with $n>1$, but also every commutative Artinian ring, and also some broader classes are included.

Answer 2

You've correctly computed the examples. The reason you keep getting $R$ for your localization is that all the elements of your $D_i$ are already units in $R$. Basically by definition $D^{-1} R$ is the "smallest" ring containing $R$ such that each element of $D$ is invertible---since these elements are already invertible in $R$, then $D^{-1}R$ is isomorphic to $R$ itself. ("Smallest" can be made precise, as I explain below.) As a note, if you restrict your $D$ to only contain non-(zero divisors) the same phenomenon will occur for $\newcommand{\Z}{\mathbb{Z}} \Z/n\Z$, as every element is either a unit or a zero divisor.

Localization satisfies the following universal property. (See here for a reference.) There is a ring homomorphism \begin{align*} \varphi: R &\to D^{-1} R\\ r &\mapsto r/1 \, , \end{align*} and, given any ring homomorphism $\psi: R \to S$ such that $\psi(D) \subseteq S^\times$, i.e., such that $\psi(d)$ is a unit in $S$ for every $d \in D$, then there is a unique ring homomorphism $\rho: D^{-1} R \to S$ such that the following diagram commutes.

$\hspace 5cm$

In your example, since all the elements of $D$ are invertible in $R$, we can apply this to the identity map $\newcommand{\id}{\operatorname{id}} \id_R: R \to R$, which yields

$\hspace 5cm$

so $\rho \circ \varphi = \id_R$. I claim that $\varphi \circ \rho = \id_{D^{-1} R}$ as well, which would show that $\varphi$ and $\rho$ are mutually inverse isomorphisms, so $R \cong D^{-1} R$.

To see this, note that $\varphi \circ \rho \circ \varphi = \varphi$. We now apply the universal property to the map $\varphi$ itself: there exists a unique homomorphism $D^{-1} R \to D^{-1} R$ such that the following diagram commutes.

$\hspace 5cm$

But we have two homomorphisms completing the diagram: the identity map $\id_{D^{-1} R}$ and $\varphi \circ \rho$. By uniqueness, then we must have $\varphi \circ \rho = \id_{D^{-1} R}$, as desired.

One can also see why $R = D^{-1} R$ in a more concrete way using elements. Since each $d \in D$ has an inverse in $R$, given $r/d \in D^{-1} R$, then $$ \frac{r}{d} = \frac{r d^{-1}}{1} \in \operatorname{img}(\varphi) $$ so every element of $D^{-1} R$ is in the image of $\varphi$, hence $\varphi$ is surjective. Since $\varphi$ is injective (here we are using the assumption that $D$ contains no zero divisors), then it is an isomorphism.