0

I've been looking for a way to measure distance in hyperbolic geometry, but I've come to a dead end-- I have to integrate this beast:$$\sqrt{\frac{\gamma^2}{(e_1e_4-e_2e_3)^2}\left((e_4+e_2\tau^{-2})^2+(-e_3-e_1\tau^{-2})^2\right)+\frac{\gamma^4[(e_4\tau-e_2\tau^{-1})(e_4+e_2\tau^{-2})+(-e_3\tau+e_1\tau^{-1})(-e_3-e_1\tau^{-2})]^2}{(e_1e_4-e_2e_3)^2((e_1e_4-e_2e_3)^2+\gamma^2[(e_4\tau-e_2\tau^{-1})^2+(-e_3\tau+e_1\tau^{-1})^2])}}\ \ d\tau.$$ I obtained this from the arclength of hyperbola in 3-space, which is the geodesic of the 2-sheet hyperboloid $x^2+y^2-z^2=-1$: the geodesics of this quadratic form are the intersections of the surface itself and planes through the origin. I was thinking to instead integrate the arclength of it in its own plane, but I thought this path would be fruitful. The hyperbola is given by

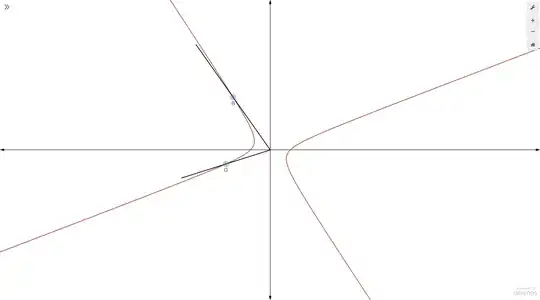
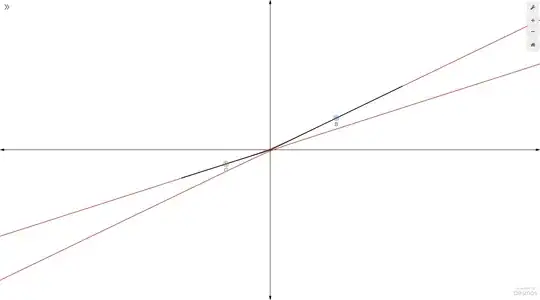
$$Hyp=\left(x,y,\pm \sqrt{x^2+y^2+1}\right)$$ with $$(\alpha^2-\gamma^2)x^2+2\alpha\beta xy+ (\beta^2-\gamma^2)y^2=\gamma^2$$ and the $e_k$ are functions of $\alpha,\beta,\gamma,\delta,$ which are functions of the coordinates $G=(x_0,y_0,z_0)$, $B=(x_1,y_1,z_1).$ Projecting the hyperbola to the $xy$-plane gives these images so you can get a feel for it:

enter image description here] enter image description here enter image description here

I'm trying to get the distance between $G$ and $B$. The integral above comes from using the metric

$$ds^2=dx^2+dy^2+\frac{(xdx+ydy)^2}{1+x^2+y^2}$$ and factoring $(\alpha^2-\gamma^2)x^2+2\alpha\beta xy+ (\beta^2-\gamma^2)y^2=\gamma^2$ like $$(e_1x+e_2y)(e_3x+e_4y)=\gamma^2\implies e_1x+e_2y=\gamma\tau\text{ and } e_3x+e_4y=\gamma\tau^{-1}$$

Any help to find the distance is appreciated! One I obtain the distance, I can then move to mapping the hyperbola to the plane.

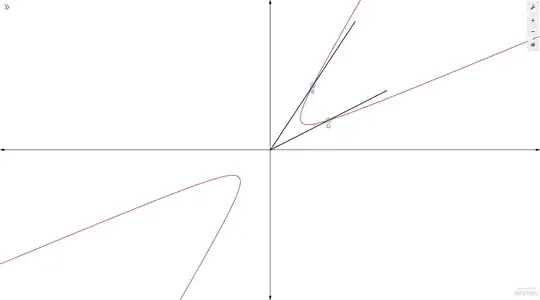Alexander Conrad
  • 1,798
  • 2
    Distance of what? What model of hyperbolic geometry? – Thomas Andrews Jan 30 '23 at 17:51
  • 1
    For starters: The two-sheeted hyperboloid has (very non-constant) positive curvature, so what does this have to do with hyperbolic geometry? – Ted Shifrin Jan 30 '23 at 18:04
  • @TedShifrin "Whereas the Gaussian curvature of a hyperboloid of one sheet is negative, that of a two-sheet hyperboloid is positive. In spite of its positive curvature, the hyperboloid of two sheets with another suitably chosen metric can also be used as a model for hyperbolic geometry." -- Wikipedia. Now, I am going to squish the space into the euclidean plane, similar to how the Poincare model is projected down to the disc. – Alexander Conrad Jan 30 '23 at 18:15
  • @ThomasAndrews I'm coming up with my own, but first I need the distance function. I've tweaked my model in contrast with the others to include the region outside of the disc, even though the disc boundary are the "points at infinity" – Alexander Conrad Jan 30 '23 at 18:16
  • 2
    Yes, you use the Lorentz metric and look at the two-sheeted hyperboloid. Where is that in your discission? P.S. See this post. – Ted Shifrin Jan 30 '23 at 18:28
  • @TedShifrin The distance function will be defined as the distance between two points in the model rather than in the hyperboloid after mapping $G$ and $B$ to the plane by the inverse of the map which takes the plane to the hyperboloid. PS I want to use the inverse map $(x,y,z)\mapsto \frac{(x,y)}{1+z}$ – Alexander Conrad Jan 30 '23 at 18:33
  • 1
    I don't understand why anything you're talking about should say we're in a two-dimensional space of constant negative curvature. – Ted Shifrin Jan 30 '23 at 18:38
  • @TedShifrin I'm assuming. But measuring the curvature is not simple, unless you have resources that could help? I know I can obtain the Ricci tensor $R_{ij}$ and compute $v^iv^jR_{ij}$ to see if independent of $v$ the scalar is $-1.$ You already said though that it should be + for the hyperboloid, but once the metric tensor is obtained intrinsic to the resulting space, then I can be sure. There seems to be an easier way using differential forms, but I'm new to this subject. – Alexander Conrad Jan 30 '23 at 18:47
  • 1
    It is not a fun computation, but Mathematica tells me that the curvature of the metric toward the end of your post is $K=\dfrac1{(1+2(x^2+y^2))^2}$. Very not hyperbolic. – Ted Shifrin Jan 30 '23 at 22:04
  • 1
    Indeed, as I suspected, this is the curvature of the hyperboloid itself, just in very awkward coordinates. – Ted Shifrin Jan 30 '23 at 22:45

0 Answers0