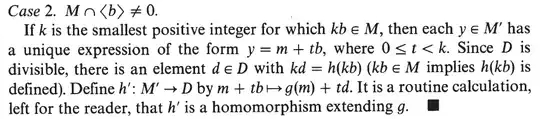0

I'm trying to generaliz this proposition: Let $G$ an abelian group and $D$ a divisible grop, for every $H\leq G$ and every homomorphism $f:H\to D$ exists $\overline{f}:G\to D$ an extension of $f$.

I want to prove in the case when $G$ is non-abelian and $H$ is a normal subgroup of $G$.

I was trying to imitate the proof of the clasic result (I put this proof below as a picture) but I have a problem in the unique expressions as sumands of the elements.

Any help or hint is welcome.

enter image description here

enter image description here

TresTresUno
  • 224

1 Answers1

0

It is no longer true for non-abelian groups.

Take any nilpotent group $G$ with $G_2 = \mathbb{Q}$. For instance take $$G:=\begin{bmatrix} 1& \mathbb{Q} &\mathbb{Q} \\ 0 &1 &\mathbb{Q} \\ 0& 0& 1\end{bmatrix}$$ then $$G_2=\begin{bmatrix} 1& 0 &\mathbb{Q} \\ 0 &1 &0 \\ 0& 0& 1\end{bmatrix}$$

Now let $H=G_2$ (it is classical that this group is normal, see e.g. How to show that the commutator subgroup is a normal subgroup) and define $\phi:G_2\rightarrow \mathbb{Q}$ be the projection to the coordinate in the top right corner. That is clearly a homomorphism.

However, any homomorphism $G\rightarrow \mathbb{Q}$ must be trivial on $G_2$ (because the image is abelian). Therefore one can not extend $\phi$ to $G$.

Yanko
  • 14,341
  • It's true, thank you very much. And what happens if instead of any divisible group $D$, a specific divisible group is taken as $\mathbb{T}$? – TresTresUno Jan 27 '23 at 21:44
  • Then take $G$ over $\mathbb{R}$ instead of $\mathbb{Q}$ and use the same construction. – Yanko Jan 27 '23 at 21:45