This can be solved through Mellin transforms.
Preliminaries. We will need two known transforms:
$$
\int_0^{+\infty} t^{s-1} e^{i\omega t - \delta|\omega t|} dt = (\delta|\omega| - i\omega )^{-s}\Gamma(s), \\ \mathrm{Re}\,s > 0, \delta > 0,\omega \in \mathbb{R},$$
and
$$
\int_0^{+\infty} \frac{\omega^{s'-1}}{1 + c \omega^{\alpha}} d\omega = \frac{1}{|\alpha|} c^{-\frac{s'}{\alpha}} \Gamma\left(\frac{s'}{\alpha}\right) \Gamma\left(1-\frac{s'}{\alpha}\right),\\ 0 < \mathrm{Re}\,\frac{s'}{\alpha} < 1,\ \alpha \in \mathbb{R},\ \alpha \neq 0,\ c\ \notin (-\infty, 0].
$$
They can be easily deduced from the definitions of the gamma and beta functions or found in tables of transforms, such as those from the Bateman Manuscript Project.
Step 1. Regularize the original integral near zero (there is a pole if $a > 1$) and at infinity (we would like to have absolute convergence to make sure that we can reorder integrations):
\begin{align}
f(t) \quad &= \lim_{\substack{\delta \rightarrow 0^{+}\\ \epsilon\,\mathrm{sgn}(a - 1) \rightarrow 0^{+}}} f_{\delta\epsilon}(t),\\ f_{\delta\epsilon}(t) \quad &= \quad \int_{- \infty}^{+ \infty} d \omega e^{i\omega t - \delta|\omega t|}
\frac{|\omega|^\epsilon}{i b | \omega |^a - \omega},\\
a \in \mathbb{R},\ a \neq 1,\ \mathrm{Re}\ b &\neq 0,\ \delta > 0,\ \min(0, a - 1) < \epsilon < \max(0, a - 1).
\end{align}
The particular choice of regularization is dictated by the desire to find the Mellin transform in closed form.
Step 2. Take Mellin transform:
\begin{align}
F_{\delta\epsilon}(s) &= \int_0^{\infty} f_{\delta\epsilon}(t) t^{s - 1} dt = \Gamma (s) \int_{- \infty}^{+
\infty} d \omega \frac{|\omega|^\epsilon}{i b | \omega |^a -
\omega} (\delta|\omega| - i\omega )^{-s} \\
&= \frac{1}{|a - 1|} \left[ (\delta + i)^{- s} (i b)^{\frac{s - \epsilon}{a -
1}} - (\delta - i)^{- s} (- i b)^{\frac{s - \epsilon}{a - 1}} \right]\\
&\times \Gamma (s) \Gamma \left( - \frac{s - \epsilon}{a - 1} \right) \Gamma \left(
1 + \frac{s - \epsilon}{a - 1} \right).
\end{align}
The double integral over $t$ and $\omega$ converges absolutely within the fundamental strip $0 < \mathrm{Re}\, s < \epsilon + 1 - a$ if $a < 1$ and $0 < \mathrm{Re}\, s < \epsilon$ if $a > 1$. You can verify it by removing $e^{i\omega t}$ and replacing the denominator with $|\omega|^a + |\omega|$.
Step 2.5. Take the limit $\delta \rightarrow 0^{+}$ (assuming $\mathrm{Re}\,b > 0$):
$$
F_{\epsilon}(s) =
- \frac{2 i}{| a - 1 |} b^{\frac{s - \epsilon}{a - 1}} \sin \left[
\frac{\pi}{2} \left( s + \frac{s - \epsilon}{1 - a} \right) \right] \Gamma
(s) \Gamma \left( \frac{s - \epsilon}{1 - a} \right) \Gamma \left( 1 -
\frac{s - \epsilon}{1 - a} \right).
$$
Extra precautions needed with $\epsilon$, because the fundamental strip vanishes in the $\epsilon \rightarrow 0$ limit if $a > 1$ due to the pole at $s = \epsilon$. If an integration contour crosses this pole when taking the limit $\epsilon \rightarrow 0$, the corresponding residue ($\pi i$) has to be subtracted. We will do it for the inverse Mellin transform.
Keeping this in mind, we can set $\epsilon$ to zero too:
$$
F(s) =
- \frac{2 i}{| a - 1 |} b^{\frac{s}{a - 1}} \sin
\left(\frac{\pi}{2}\frac{2 - a}{1 - a}s \right) \Gamma
(s) \Gamma \left( \frac{s}{1 - a} \right) \Gamma \left( 1 -
\frac{s }{1 - a} \right).
$$
Step 3. Apply the identity $\frac{\pi}{\sin(\pi z)} = \Gamma(z) \Gamma(1-z)$ and its corollary $\Gamma(z) \Gamma(1-z) = -\Gamma(-z) \Gamma(1+z)$:
$$
F(s) =
\frac{2 \pi i}{ |a - 1| }\mathrm{sgn}(a-2) b^{\frac{s }{a - 1}} \Gamma
(s) \frac{\Gamma \left( \frac{s}{|a - 1|} \right) \Gamma \left( 1
- \frac{s}{|a - 1|} \right)}{\Gamma \left( \frac{1}{2} \left|\frac{2-a}{a-1}\right| s \right) \Gamma \left( 1 -
\frac{1}{2} \left|\frac{2-a}{a-1}\right| s \right)}.
$$
We need this particular choice of signs in the gamma functions to be able to choose an integration path consistent with the definition of the Fox H-function.
Step 4. Take inverse Mellin transform:
\begin{align}
& f(t) = \frac{1}{2 \pi i} \int_{c - i \infty}^{c + i \infty} t^{- s} F (s) d s -\pi i\, \theta(a - 1) =
\frac{1}{2 \pi i} \int_{- c - i \infty}^{- c + i \infty} t^s F (- s) d s -\pi i\, \theta(a - 1)\\ &=
\frac{2 \pi i\, \mathrm{sgn} (a - 2)}{|a - 1|} H^{21}_{23} \left( b^{\frac{1}{1 -
a}} t\ \middle| \begin{array}{ccc}
& \left( 0, \frac{1}{| a - 1 |} \right) & \left( 0, \frac{1}{2} \left|
\frac{2 - a}{a - 1} \right| \right)\\
(0, 1) & \left( 0, \frac{1}{| a - 1 |} \right) & \left( 0, \frac{1}{2}
\left| \frac{2 - a}{a - 1} \right| \right)
\end{array} \right) -\pi i\, \theta(a - 1)
\end{align}
(by definition of the Fox function, assuming positive real $b$).
If $c$ is chosen between $0$ and $|a - 1|$, integration path stays within the fundamental strip in the $\epsilon \rightarrow 0$ limit if $a < 1$ and crosses a pole at $s = \epsilon$ if $a > 1$. The residue at this pole provides the last term.
Swapping integration with $\lim$ can be justified by the dominated convergence theorem. For example, at $\mathrm{Im}\,s \rightarrow \infty$ $|F_{\delta\epsilon}(s)| < \mathrm{const} \times e^{- \frac{1}{2} \left| \arg (- b^2) \frac{\mathrm{Im}\,s}{a - 1} \right|}$ for any sufficiently small $\delta, \epsilon$ within the allowed range.
Step 5. Repeat for $t<0$ (equivalent to $b < 0$ because $f(-t; b) = - f(t; -b)$):
\begin{align}
f(t) = - \frac{2 \pi i\, \mathrm{sgn} (a)}{|a - 1|} H^{21}_{23} \left( b^{\frac{1}{1 -
a}} |t|\ \middle| \begin{array}{ccc}
& \left( 0, \frac{1}{| a - 1 |} \right) & \left( 0, \frac{1}{2} \left|
\frac{a}{a - 1} \right| \right)\\
(0, 1) & \left( 0, \frac{1}{| a - 1 |} \right) & \left( 0, \frac{1}{2}
\left| \frac{a}{a - 1} \right| \right)
\end{array} \right) + \pi i\, \theta(a - 1)
\end{align}
Step 6. Check numerically.
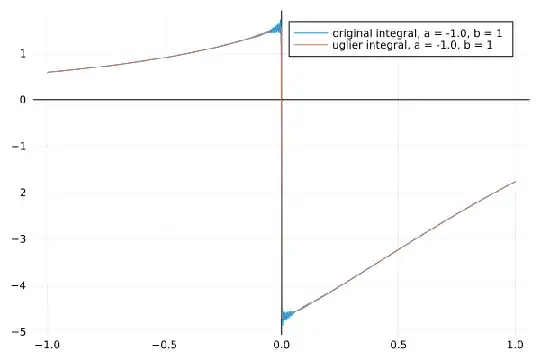
You can find alternative expressions by a change of variables $t' = t^{|a - 1|}$ or by rewriting sine through exponentials instead of gamma functions.
This idea has been applied by Schneider to a similar problem involving $e^{-|\omega|^a}$ in the context of stable distributions. A few more relevant references here.
