26

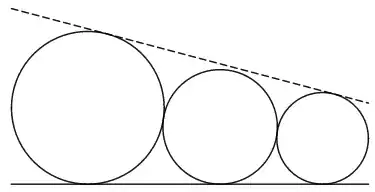
Three disks are placed on the ground like this:

enter image description here

From left to right, their radii are $\frac{1}{x-1}, \frac{1}{x}, \frac{1}{x+1}$ metres. They lie in a plane perpendicular to the ground. The middle disk touches the other two disks.

Using only paper and pen, approximate the value of $x$ such that the middle disk is tangent to the line that is tangent to and above the other two disks. You may assume that the earth is a sphere of radius $R$ metres.

(Before you read the last sentence, it seems like there's something wrong with the question, because it seems like the middle disk should never touch the line. But the ground is actually a circular arc of the earth, so the middle disk is "pushed up" and touches the line for some value of $x$.)

The answer turns out to be, elegantly, $x\approx R/2$. But the algebra seems to be horrendous and I needed to use my computer to find the answer.

My attempt

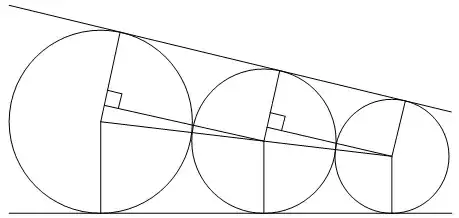
enter image description here

Call the angles at the centre of the middle disk $A, B, C, D, E$ with $A$ at the lower-left and going clockwise.

$A=\arccos{\left(\dfrac{\left(\frac{1}{x}+\frac{1}{x-1}\right)^2+\left(R+\frac{1}{x}\right)^2-\left(R+\frac{1}{x-1}\right)^2}{2\left(\frac{1}{x}+\frac{1}{x-1}\right)\left(R+\frac{1}{x}\right)}\right)}$

$B=\arcsin{\left(\dfrac{\frac{1}{x-1}-\frac{1}{x}}{\frac{1}{x-1}+\frac{1}{x}}\right)}$

$C=\dfrac{\pi}{2}$

$D=\arccos{\left(\dfrac{\frac{1}{x}-\frac{1}{x+1}}{\frac{1}{x}+\frac{1}{x+1}}\right)}$

$E=\arccos{\left(\dfrac{\left(\frac{1}{x}+\frac{1}{x+1}\right)^2+\left(R+\frac{1}{x}\right)^2-\left(R+\frac{1}{x+1}\right)^2}{2\left(\frac{1}{x}+\frac{1}{x+1}\right)\left(R+\frac{1}{x}\right)}\right)}$

We assume that the middle disk is tangent to the line that is tangent to and above the other two disks. This implies:

$$A+B+C+D+E=2\pi$$

I am utterly unable to approximate $x$ without a computer, even after attempting to simplify it. And yet the computer-assisted answer is just $x\approx R/2$. Can $x$ be approximated without a computer?

(This question was inspired by a frame challenge.)

Dan
  • 35,053
  • 2
    Just to clarify: the "flat line" at the base of you diagrams is actually part of a circle with radius $R$, right? – David Jan 15 '23 at 11:28
  • @David Yes, that's right. It's the ground, which is a circular arc of the earth. I'll add this clarification into the question. – Dan Jan 15 '23 at 11:30
  • 1
    Hi there, could you elaborate on your comment "... the line for sufficiently large values of x" because it feels like as x becomes very Large the radii become extremely small, thereby the curvature of the ground they are placed on becoming insignificant. – mrtechtroid Jan 15 '23 at 12:59
  • @mrtechtroid Imagine wrapping the earth with a taut string, except the string goes over the disks (in the same plane as the disk). Where the disks are very small, the string touches every disk. So if we have three consecutive very small disks, and we draw a line that is tangent to and above the left and right disks, the disk in the middle must intersect this line. – Dan Jan 15 '23 at 13:22
  • @mrtechtroid Here's another way of looking at it. If the disks are the exact same size, then the curvature of the earth causes the middle disk to be slightly "higher" than the other two disks. As the disks get smaller, their sizes get closer to being the same size. – Dan Jan 15 '23 at 13:49
  • 1
    Computer construction of this https://www.geogebra.org/classic/qhkzy2qt – James K Jan 15 '23 at 22:41
  • @JamesK Nice construction. But it looks like, when $r<2$, circle $C$ loses contact with the line. I think the three circles should be able to touch the line as long as $r>1/2$. – Dan Jan 15 '23 at 22:59
  • 2
    that't correct. This uses the x= R/2+1/R approximation for the answer below. This approximation is very good for R>4, but isn't a good approximation for small values of R. It is implied that R is very large in this question. @Dan – James K Jan 15 '23 at 23:15
  • 3
    FYI: Using more than paper and pen, one can show that, for an Earth of radius $r$ and tangent circles of radius $p$, $s$, $q$ (in that order), those last circles have a common tangent line when $$(p-q)^2s^4-8pqrs^2(p+q+2s)+16pqr^2(pq-s^2)=0$$ If $p=1/(x-1)$, $s=1/x$, $q=1/(x+1)$, this becomes something we can write as $$8y^2\left(y-\frac12\right)=\frac4{r^2}y+\frac1{r^4} \qquad\qquad y:=\frac{x}{r}$$ If $y$ is roughly constant for large $r$, then as the right-hand side becomes negligible, we find $y=0$ or $y=1/2$. – Blue Jan 16 '23 at 05:44
  • @Blue. You inspired me ! Thanks for the solution you gave. Cheers :-) – Claude Leibovici Jan 16 '23 at 15:31

2 Answers2

13

They simplify to $$A=\frac\pi2+\arcsin\frac{\left(R+\frac1x\right)-2}{\left(R+\frac1x\right)(2x-1)}\\ B=\arcsin\frac1{2x-1}\\ C=\frac\pi2\\ D=\frac\pi2-\arcsin\frac1{2x+1}\\ E=\frac\pi2-\arcsin\frac{\left(R+\frac1x\right)+2}{\left(R+\frac1x\right)(2x+1)} $$ Suppose $x=O(R)$.
All four key angles turn out to be $O(1/R)$, which is small enough that I can ignore the arcsine at the precision I need, which is $O(1/R^3)$. Since the $O(1/R)$ terms cancel exactly, the nonlinear $O(1/R^3)$ terms in arcsines will cancel as well.
$$A\approx\frac\pi2+B-\frac2{\left(R+\frac1x\right)(2x-1)}\\ B+D\approx\frac\pi2+\frac2{4x^2-1}\\ E\approx D-\frac2{\left(R+\frac1x\right)(2x+1)}\\ A+B+C+D+E\approx2\pi+\frac4{4x^2-1}\left(1-\frac{2x}{R+\frac1x}\right)$$ So my leading order estimate is $$x\approx\frac R2+\frac1R$$

Empy2
  • 52,372
12

Using the solution given by @Blue in comments, it is not difficult to solve exactly the cubic equation in $y$ provided that we use the hyperbolic solution.

Using only pen and paper, the exact result is $$\color{blue}{y=\frac 16 +\frac{\sqrt{r^2+6}}{3 r}\cosh \left(\frac{1}{3} \text{sech}^{-1}\left(\frac{2 r \left(r^2+6\right)^{3/2}}{2 \left(r^2+9\right) r^2+27}\right)\right)}$$ which must be very close to an hyperbola.

Using a computer, expanding for large values of $r$

$$y=\frac 12 + \frac 1 {r^2}\left( 1-\frac{3}{2 r^2}+\frac{5}{r^4}+O\left(\frac{1}{r^6}\right)\right)$$ that is to say $$x=\frac r2 + \frac 1 {r}\left( 1-\frac{3}{2 r^2}+\frac{5}{r^4}+O\left(\frac{1}{r^6}\right)\right)$$

as already given by @Empy2 using simple and legitimate approximations.

mathlander
  • 4,097
Claude Leibovici
  • 289,558
  • 1
    +1 ... and you inspired me to take another look at that root of the cubic. Mathematica's solution was rather messy, so I sought to avoid giving it. However, I have now managed to wrangle it into this form: $$y=\frac16\left(1+\sqrt[3]{1+u_+}+\sqrt[3]{1+u_-}\right)\qquad u_{\pm}:=\frac{18r^2+27\pm3\sqrt{3(4r^2+27)}}{2r^4}$$ For large $r$, we clearly have $u_{\pm}\approx 0$, so that $y\approx 1/2$. Done! (Full disclosure: More than pen-and-paper was used to arrive at the $pqrs$ relation that gave rise to the cubic. Maybe there's a more straightforward path to it.) – Blue Jan 16 '23 at 16:26
  • 2
    @Blue. If I may suggest, never use this formula. It gives monsters; Use the trigonometric method for 3 real roots and the hyperbolic method for one real solution. – Claude Leibovici Jan 17 '23 at 03:46