This is a sequel to my highly upvoted question (at the time of writing, my third-best post).
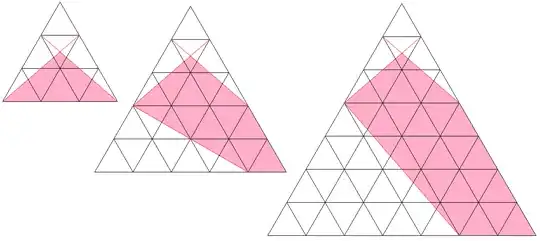
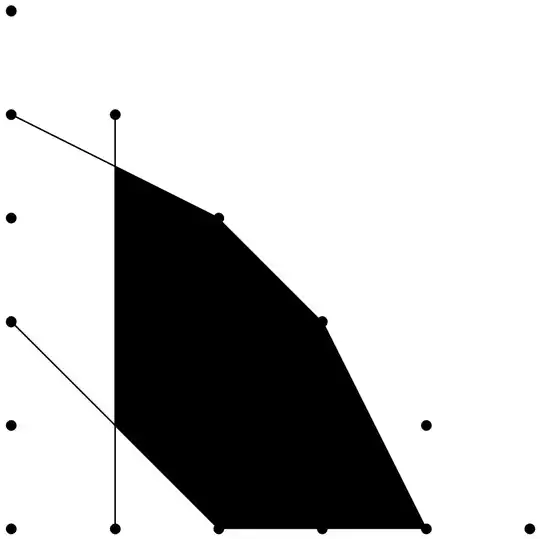
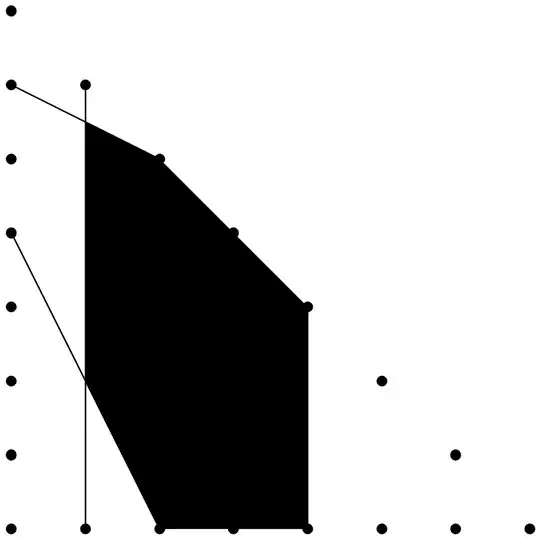
Let there be an equilateral triangle that has $n+1$ notches on each edge (corners included) to divide each edge into $n$ equal parts. We can make cuts on the triangle from notch to notch. Is it always possible to cut out a connected piece with area $\frac{1}{2}$ the area of the original triangle if $n≥2?$ It is possible for multiples of $2$ or $3,$ but I don't know any other numbers for which this is possible. If it is possible for $n,$ it is possible for any multiple of $n.$
For simplicity, in my answers and comments (and in the solution for $3$), I'd use a transformed version of the coordinate system so that the vertices of the triangle are $(0,0), (n,0),$ and $(0,n).$ Since this is a linear transformation, it has constant determinant, so ratios of areas won't be affected.
$2$: Cut along a median.
$3$: Cut from $(0,1)$ to $(3,0)$ and $(0,3)$ to $(1,0),$ then take the piece with the diagonal side as one of its sides.