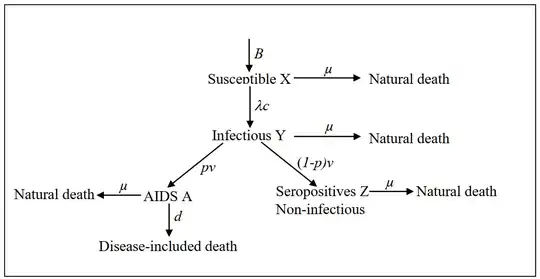
AIDS epidemic in a homosexual population
The following diagram shows the AIDS epidemic in a homosexual population:
Then the model can be described by $$ \begin{gathered} d X / d t=B-\mu X-\lambda c X \\ d Y / d t=\lambda c X-(v+\mu) Y \\ d A / d t=p v Y-(d+\mu) A \\ d Z / d t=(1-p) v Y-\mu Z \\ \textrm{Where }N(t)=X(t)+Y(t)+Z(t)+A(t) \end{gathered} $$
The system evolves to a steady state given by
$$ \begin{aligned} X^*&=\frac{(v+\mu) N^*}{c \beta},\\Y^*&=\frac{(d+\mu)\left(B-\mu N^*\right)}{p v d},\\ Z^*&=\frac{(1-p)(d+\mu)\left(B-\mu N^*\right)}{p d \mu},\\ A^*&=\frac{\left(B-\mu N^*\right)}{d},\\ N^*&=\frac{B \beta[\mu(v+d+\mu)+v d(1-p)]}{(v+\mu)[\beta(d+\mu)-p v]} . \end{aligned} $$
But the problem is, I can solve the $\frac{dX}{dt}=0,\frac{dY}{dt}=0,\frac{dA}{dt}=0,\frac{dZ}{dt}=0$ simultaneously but couldn't bring the format of those states. I need to do this computation in the exam, so it will be a great help if anyone gives any suggestions or ways to make the computation quick.