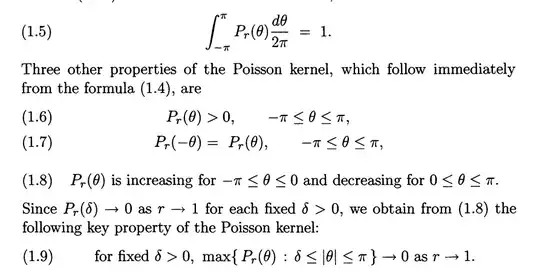The problem is from Gamelin exercise X.1.6.
A function $f(z),z\in\Bbb D$ is said to have radial limit $L$ at $\zeta\in\partial\Bbb D$ if $f(r\zeta)\to L$ as $r$ increases to $1$. Let $h(e^{i\theta})$ be a piecewise continuous function on the unit circle. Show that $\tilde{h}(z)$ has a radial limit at each $\zeta\in\partial\Bbb D$, equal to the average of the limits of $h(e^{i\theta})$ as $\zeta$ from each side. Here, $\tilde{h}(z) =\int_{-\pi}^\pi h(e^{i\varphi})P_r(\theta-\varphi){d\varphi\over 2\pi}$ for $z = re^{i\theta}\in\Bbb D$ and $P_r(\theta) = \operatorname{Re}\left({1+z\over 1-z}\right)$, $z\in\Bbb D$ which is a Poisson kernel.
I think we need to assume that all discontinuities are jump discontinuities. Let $\zeta = e^{i\theta}$ and define
$$h_+(e^{i\theta}) = \lim_{\varphi\to 0+}h(e^{i(\theta+\varphi)}),\quad h_{-}(e^{i\theta}) = \lim_{\varphi\to 0+}h(e^{i(\theta-\varphi)}).$$
So the claim is
$$\lim_{r\to 1+}\tilde{h}(r\zeta) = {1\over 2}(h_+(e^{i\theta})+h_-(e^{i\theta})).$$
Fix $0<r<1$ and consider
$$\tilde{h}(re^{i\theta})-{1\over 2}(h_+(e^{i\theta})+h_-(e^{i\theta})) = {1\over 2\pi}\int_{-\pi}^\pi\left(h(e^{i(\theta-\varphi)}-{1\over 2}(h_+(e^{i\theta})+h_-(e^{i\theta}))\right)P_r(\varphi)\ d\varphi.\quad(\dagger)$$
Choose small $0<\delta$ so that $|h_+(e^{i\theta}) - h(e^{i(\theta+\varphi)})|<\epsilon$ and $|h_-(e^{i\theta}) - h(e^{i(\theta-\varphi)})|<\epsilon$ for all $0\leq\varphi\leq\delta$. Then,
\begin{align*}
(\dagger)\leq{1\over 2\pi}\left(\int_{-\delta}^{\delta}+\int_{\delta\leq|\varphi|\leq\pi}\right)\left({1\over 2}|h(e^{i(\theta-\varphi)})-h_+(e^{i\theta})|+{1\over 2}|h(e^{i(\theta-\varphi)})-h_-(e^{i\theta})|\right)P_r(\varphi)\ d\varphi\\
\leq {1\over 4\pi}\int_{-\delta}^\delta|h(e^{i(\theta-\varphi)})-h_+(e^{i\theta})|P_r(\varphi)\ d\varphi+{1\over 4\pi}\int_{-\delta}^\delta|h(e^{i(\theta-\varphi)})-h_-(e^{i\theta})|P_r(\varphi)\ d\varphi+o(r).\\
\end{align*}
where the last inequality follows from the fact that $\max_{\delta\leq|\varphi|\leq\pi}P_r(\varphi)\to 0$ as $r\to 1$.
Note that
\begin{align*}
& {1\over 4\pi}\int_{-\delta}^\delta|h(e^{i(\theta-\varphi)})-h_+(e^{i\theta})|P_r(\varphi)\ d\varphi\\
& = {1\over 4\pi}\left(\int_{-\delta}^0|h(e^{i(\theta-\varphi)})-h_+(e^{i\theta})|P_r(\varphi)\ d\varphi+{1\over 4\pi}\int_0^\delta|h(e^{i(\theta-\varphi)})-h_+(e^{i\theta})|P_r(\varphi)\ d\varphi\right).
\end{align*}
First integral can be bounded by $\epsilon$ by the assumption of $\delta$ but the second integral cannot be bounded by a constant multiple of $\epsilon$. I'm stuck at this point. The hint is to use the symmetric property of $P_r(\varphi)$, i.e., $P_r(-\varphi) = P_r(\varphi)$ for $-\pi\leq\varphi\leq\pi$ but I don't know how to use it. Please help.
N.B. The above argument is following the proof given in the textbook (I'll just attach it as an image. I think it's ok):
Some properties I used (possibly) without mentioning:
