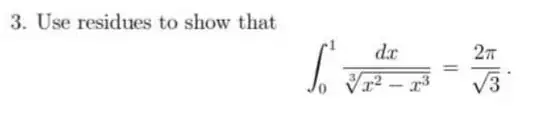You can not say that $0$ and $1$ are poles. Those singularities are not isolated. The first difficulty is to have a well-defined holomorphic function. There is no holomorphic function on $\mathbb{C}^*$ transforming every non-zero complex number into one of its cubic roots.
But you may consider $L$ the principal determination of logarithm on $\mathbb{C} \setminus \mathbb{R}_-$, and the function $\exp(L/3)$ is holomorphic on $\mathbb{C} \setminus \mathbb{R}_-$ and provides a cubic root.
An idea is to write $z^2-z^3 = -z^3(1-1/z)$ and set
$$f(z) := -\frac{1}{z \exp(L(1-1/z)/3)} \textrm{ for all } z \in \mathbb{C} \setminus [0,1].$$ This is well-defined since $1-1/z \notin \mathbb{R}_-$, and by compositon, we get an holomorphic function on $\mathbb{C} \setminus [0,1]$. Observe that
$$f(z)^3 = -\frac{1}{z^3 \exp(L(1-1/z))} = -\frac{1}{z^3(1-1/z)} = \frac{1}{z^2-z^3}.$$
Next difficulty: which contour use? A contour with two pieces should work, a large circle $C(0,R)$ with $R>>1$ and a thin saussage made with the segments $[\epsilon i,1+\epsilon i]$ and $[-\epsilon i,1-\epsilon i]$, and two half circles with center $0$ and $1$ and with radius $\epsilon$ each (make a picture). The saussage part turns around the segment $[0,1]$ and remains at distance $\epsilon$ to this segment.
Because $f$ is holomorphic on $\mathbb{C} \setminus [0,1]$, the curving integral along the circle $C(0,R)$ and along the saussage part are equal.
Then you let $R$ go ton infinity and go the the limit, using repeatedly Lebesgue dominated convergence theorem.
Since $zf(z) \to -1$ as $z \to \infty$, the integral along the circle $C(0,R)$ has a non-trivial limit as $R \to +\infty$.
Since $zf(z) \to 0$ as $z \to 0$ and $(z-1)f(z) \to 0$ as $z \to 1$, the integral along the two half-circles centered at $0$ and at $1$ tend to $0$ as $\epsilon \to 0$.
When $\epsilon \to 0$ and $x \in [0,1]$, $f(x \pm \epsilon i)$ tends to some cubic root of $1/(x^2-x^3)$. We have to look carefully which one, it can be $1/\sqrt[3]{x^2-x^3}$ or $e^{i2\pi/3}/\sqrt[3]{x^2-x^3}$ or $e^{-i2\pi/3}/\sqrt[3]{x^2-x^3}$. Hence the integral on the segments $[\epsilon i,1+\epsilon i]$ and $[-\epsilon i,1-\epsilon i]$ have a limit which is $1$ or $e^{i2\pi/3}$ or $e^{-i2\pi/3}$ times the integral that you want to compute.