2

I'm reading about differential forms and I have the following example. Let $M= \{(x,y,z) \in \Bbb R^3 \mid x^2+y^2+z^2 < 1 \}$ and consider the $2$-form $\omega = x dy \wedge dz - y dx \wedge dz+zdx \wedge dy.$ We can now integrate $\omega$ over $\partial M$ as follows.

We have that $$\begin{align*}dx &= \cos(u)\cos(v)du - \sin(v)\sin(u) dv \\ dy &= \cos(u)\sin(v)du + \cos(v)\sin(u) dv \\ dz &= -\sin(u)du \end{align*}$$

and the wedge products are $$\begin{align*}dx \wedge dy &= \cos(u)\sin(u)du \wedge dv \\ dx \wedge dz &= -\sin(v)\sin^2(u) du \wedge dv \\ dy \wedge dz &= \sin^2(u)\cos(v)du \wedge dv \end{align*}$$

and we get that $\omega = \sin(u) du \wedge dv.$ Thus integrating $$\int_{\partial M} \omega = \int_{0}^{2\pi}\int_{0}^\pi \sin(u) dudv = 4\pi.$$

What I don't get here is that what is the interpretation of this $2$-form $\omega$. I can see that the integral checks out by looking at the definitions, but I have no understanding what is $\omega$ representing.

What is the use of integrating over something that one cannot understand. Even in this case we're just integrating something over the boundary of the unit disc in $\Bbb R^3$ and yes the output is some number, but I have no idea what can I conclude from this.

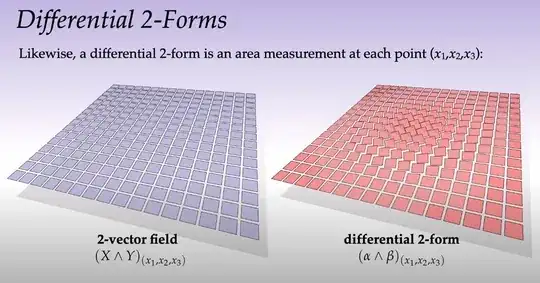
I have been watching this lecture series by Keenan Crane and he does a really nice job on visualizing these things, but it's still not clicking for me quite yet.

He's given the following visualizations and what I'm trying to do is to figure out how they apply for example in the integral above. Can this even be done?

enter image description here

enter image description here

Walker
  • 1,462
  • 4
  • 9
  • 1
    Are you sure your manifold is not $S^2={(x,y,z)\in\mathbb R^3:x^2+y^2+z^2\color{red}=1},?$ If so, you will find an answer here. "Volume" in that case means surface. As we know, the total surface of $S^2$ is $4\pi,.$ Edit: I see you wrote $\partial M$ which is correctly $S^2.$ – Kurt G. Jan 06 '23 at 11:23
  • to understand what is going on you can transform the integral locally to an integral over some open subset of $\mathbb{R}^2$. Also some time ago I've written an intuitive way to think about these abstract integrals, see here –  Jan 06 '23 at 11:38
  • An interpretation of $\omega$ is the following: $\omega_p(u,v) = \det(p,u,v)$ where $p$ is the position vector field $p=(x,y,z)$. Note that the position vector field is the outward pointing unit normal to the unit sphere – Didier Jan 06 '23 at 11:51
  • So $\omega$ at a point $p$ gives the signed volume of the parallelpiped spanned by $p,u$ and $v$. I cannot grasp this position vector field idea. Isn't $p$ supposed to be just a point on $\partial M$? @Didier – Walker Jan 06 '23 at 11:59
  • In $\Bbb R^n$, you are authorized (and often encouraged) to identify points with vectors, and in this case, a point in $\partial M$ is nothing less than a unit vector. – Didier Jan 06 '23 at 12:00
  • By the way, if you know Stokes Theorem, you can use the fact that $\int_{\partial M} \omega = \int_M d\omega$, and you will find that this integral is three times the volume of the three dimensional unit sphere, which is $4\pi$. – Didier Jan 06 '23 at 12:03
  • 1
    of the unit ball * – Didier Jan 06 '23 at 12:09
  • If you restrict this form to the sphere of radius $r$ centered at the origin, it is $r$ times the area form of the sphere. You might want to look at some of my videos on forms and integration over submanifolds of $\Bbb R^n$ (see my profile) – Ted Shifrin Jan 07 '23 at 02:38

1 Answers1

1

what is the interpretation of this $2$-form $\omega$

You have the volume 3-form $dV$ on the $\mathbb{R}^{3}$ which finds the signed volume of the parallelpiped spanned by a 3-vector (the determinant formula). Feeding it a unit vector makes the resulting 2-form essentially measure areas orthogonal to that unit vector.

For a surface $i:S^{2}\rightarrow \mathbb{R}^{3}$ the 2-form measuring areas is given by $$ds=i^{*}(n\lrcorner dV),$$ with interior product (contraction) and the pull-back (restriction) operations. The normals on the unit-sphere are $n=(x,y,z)$; the linearity of interior product gives

$$ds=x\ \partial_{x} \lrcorner dV+y\ \partial_{y} \lrcorner dV+z\ \partial_{z} \lrcorner dV.$$

Now remember that $dV=dx\wedge dy\wedge dz=dy\wedge dz\wedge dx=dz\wedge dx\wedge dy$; so contracting $dV$ with $\partial_{x^{i}}$ just removes the $dx^{i}$. Thus $$ds=x\ dy\wedge dz+y\ dz\wedge dx+z\ dx\wedge dy.$$

Integration intuitively is the limit process of feeding this 2-form with infinitesimal tangent 2-vectors and summing up all the measured infinitesimal areas.

rych
  • 4,445