Find, from first principles, the gradient of the tangent to the curve $y = 5 - x^2$ at the point $(1,4)$ on the curve.
So I'm currently lost on this question can some one please show me the solutions of how to complete this question and i may use it as an guide for future question. Thanks a lot!
By first principles, perhaps you mean you need to use the definition of the derivative, $$f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$$ to find the slope (i.e. gradient) of the tangent line to the curve at the point $(1, 4)$, where the curve in question is given by:
$$y = f(x) = 5 - x^2$$
$$\begin{align} f'(x) =\lim_{h \to 0} \frac{f(x + h) - f(x)}{h} & = \lim_{h \to 0} \frac{\Big(5 - (x + h)^2\Big) - (5 - x^2)}{h} \\ \\ & = \lim_{h\to 0}\frac{5 - (x^2 + 2hx + h^2) - 5 + x^2}{h} \\ \\ & = \lim_{h\to 0}\frac {-2hx - h^2}{h} \\ \\ & = \lim_{h\to 0}\frac{-h(2x + h)}{h} \\ \\ & = \lim_{h\to 0} -(2x + h)\\ \\ f'(x) & = -2x \end{align}$$
Now, at $(1, 4), \;x = 1$, so the slope or gradient at that point is given by $f'(1) = -2(1) = -2$.
Below, I've posted an image of the line tangent to the curve $y = 5 - x^2$ at the point $(1, 4)$, along with the the curve itself. (Image compliments of WolframAlpha).
Side note:
We can find the equation line tangent to $y = 5-x^2$ at the point $(1,4)$ knowing the slope of the line is $-2$, and the fact that $(1, 4)$ lies on that line. We know the equation of a line can be written in the form $(y - y_0) = m(x - x_0)$, where $m$ represents the slope of the line, and $(x_0, y_0)$ represents a point on the line.
In our case, we've found slope to be given by $-2$, and $(x_0, y_0) = (1, 4)$. So, $$y - 4 = -2(x - 1) \iff y - 4 = -2x + 2 \iff y = 6 - 2x$$
$f`(x)= -2x$...(power rule, constant becomes zero) point $(1,4)$, meaning $x=1$ and $y=4$ substitute $x=1$ in $f`(x)$ to obtain $f`(1)= -2(1)=-2$ therefore slope of the tangent line is $m=-2$ $$y=mx+c$$ $$4=-2(1)+c$$ $$4= -2+c$$ $$4+2=c$$ $$c=6$$ $$y=-2x+6$$
For the very first principles go back to Archimedes: choose two points on the parabola with equidistant first coordinates to $1$, for example $(0,5)$ and $(2,1)$. From Archimedes we know that the slope of the tangent in $x=1$ is the slope of the straight line through those points, namely $-2$.
Since if you use the derivative, you are taking for granted that the derivative exists at the point $(1, 4)$, we might also use another approach that relies on that assumption, too, but avoids the use of the derivative.
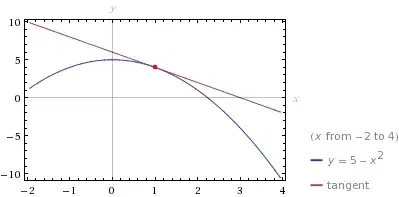
We observe that a tangent line is also a line that (a) touches the curve in question at the specified point, and (b) is everywhere else one side or the other of the curve (either above or below)*. Criterion (a) is satisfied trivially by any line that goes through point $(1, 4)$, since $4 = 5-1^2 = 5-1$.
Now, we will consider two different forms of lines passing through $(1, 4)$. The first is simply the line $x = 1$. However, it can be seen that this line contains the points $(1, 3)$ and $(1, 5)$, and since those two points lie below and above the curve, respectively, the line $x = 1$ is not tangent to that curve.
The second form is the more general equation
$$ y-4 = m(x-1) $$
which we might rewrite as
$$ y = mx+(4-m) $$
If we subtract the quadratic from the linear equation, we get
$$ \Delta y = x^2+mx-(m+1) $$
This is a parabola that we "want" to have one double root in order for the line to be tangent to the original curve $y = 5-x^2$. According to the quadratic formula, this parabola has one double root when the determinant $m^2+4(m+1) = 0$. That is,
$$ m^2+4m+4 = 0 $$
which yields the unique solution $m = -2$. Therefore, the equation of the tangent line must be $y = 6-2x$. We can verify that this line is tangent by observing that the difference $\Delta y$ is given by
$$ \Delta y = x^2-2x+1 = (x-1)^2 $$
which is always positive, so the line is always above the parabola.
*If we insist on rigor, this answer is incomplete, since we have not shown that the parabola does indeed divide the plane into two portions, above and below (and there may be other things I've missed besides, depending on your standards).
