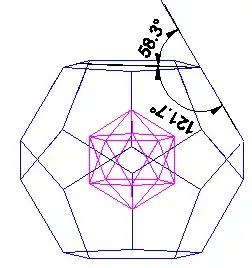
In an effort to build a dodecahedron frame in Fusion360 I need to know some of the angles. Looking around I found out that the angle between an edge and a face on a regular dodecahedron is $121.7^\circ$ but I couldn't find the mathematical formula nor the way to calculate this angle. The formula is needed so the exact angle can be used so the simulation is precise. Can anyone help?
Make a small sphere, using a vertex of the dodecahedron as the centre of the sphere. The intersection of the sphere surface and the dodecahedron surface is a triangle, whose edges are circular arcs with length $108^\circ$ (the angle in a pentagon). The angle $\phi$ you seek is the altitude of this triangle; that's the length of the arc connecting a vertex of the triangle (corresponding to an edge of the dodecahedron) perpendicularly to the opposite edge of the triangle (corresponding to a face of the dodecahedron). The spherical law of cosines, applied to the triangle cut in half, gives
$$\cos\phi=\cos108^\circ\cos54^\circ+\sin108^\circ\sin54^\circ\cos\theta,$$
where $\theta$ is the dodecahedron's dihedral angle, which in turn is given by the spherical law of cosines applied to the whole triangle:
$$\cos108^\circ=\cos108^\circ\cos108^\circ+\sin108^\circ\sin108^\circ\cos\theta$$ $$\cos\theta=\frac{\cos108^\circ-\cos^2 108^\circ}{\sin^2 108^\circ}.$$
I assume you know that the regular pentagon angle has $\cos108^\circ=-\tfrac12\varphi^{-1}$ and $\sin108^\circ=\tfrac12\sqrt{\varphi\sqrt5}$, where $\varphi=\tfrac12(1+\sqrt5)$ is the golden ratio. So we get
$$\cos\theta=-\frac{\sqrt5}{5},$$ $$\cos\phi=\left(-\tfrac12\varphi^{-1}\right)\left(\tfrac12\sqrt{\varphi^{-1}\sqrt5}\right)+\left(\tfrac12\sqrt{\varphi\sqrt5}\right)\left(\tfrac12\varphi\right)\left(-\frac{\sqrt5}{5}\right)$$ $$=-\sqrt\frac{\varphi^{-1}}{\sqrt5}\quad=-\sqrt\frac{5-\sqrt5}{10}.$$
First, define the golden ratio and its reciprocal
$$ a:=(1+\sqrt{5})/2, \quad b:=1/a=a-1. $$
From the Wikipedia article regular dodecahedron, define the six dodecahedron vertices $$ v_1 = (0,a,b),\; v_2 = (0,a,-b),\; v_3 = (1,1,-1),\\ v_4 = (a,b,0),\; v_5 = (1,1,1),\; v_6 = (a,-b,0) $$ where $\{v_1,v_2,v_3,v_4,v_5\}$ are the vertices of a pentagonal face and $v_6-v_4$ is an edge vector. Let $v_0 := (v_1+v_2)/2 = (0,a,0)$ be the midpoint of the edge of the face opposite to $v_4$. Then the acute angle $\theta$ between $w_1 := v_0-v_4 = (-a,1,0)$ and $w_2 := v_4-v_6 = (0,2b,0)$ can be computed from $$ c := \cos(\theta) = \frac{|w_1\cdot w_2|}{|w_1|\,|w_2|} = \frac{2b}{\sqrt{a^2+1}(2b)}= \frac1{\sqrt{a^2+1}} = \sqrt{\frac{5-\sqrt{5}}{10}}. $$ Note that $ c \approx 0.5257311121 $ and $\theta \approx 58.2825255^\circ$ while the angle between a face and an edge it adjoins is $180^\circ-\theta.$
Note the advantage of this method is that it needs only the coordinates of a few vertices using the golden ratio, the dot product of vectors, and no trigonometry except at the very end to get $\theta$ from its cosine.
It is maybe not a good habit to use short-cut formulas/constructions from Wikipedia, since a real mathematician should construct his geometric or analytic geometric figures herself/himself, however, I believe that it is necessary when you have not enough time.
Wikipedia already constructed a dodec with 20 vertices: $(\pm 1,\pm 1, \pm 1), (0,\pm\phi,\pm\phi^{-1}), (\pm\phi^{-1},0,\pm\phi), (\pm\phi,\pm\phi^{-1},0).$
I considered the face given by the plane $x+\phi y=\phi^2$ which has vertices, $(1,1,1),(1,1,-1),(\phi,\frac{1}{\phi},0)$, $(0,\phi,\frac{1}{\phi}),(0,\phi,-\frac{1}{\phi})$ and with normal vector $\vec n=\langle1,\phi,0\rangle$.
An edge really connects the vertices $P=(1,1,1)$ and $Q=(\frac{1}{\phi},0,\phi)$. And by using $\frac{1}{\phi}=\phi-1$, we have $\vec{PQ}=\langle \phi-2,-1,\phi-1\rangle$.
Now, we will find the angle between $\vec n$ and $\vec{PQ}$: $$\langle1,\phi,0\rangle\cdot\langle \phi-2,-1,\phi-1\rangle=\sqrt{1+\phi^2}\sqrt{(\phi-2)^2+(-1)^2+(\phi-1)^2}\cos\theta$$ $$-2=\sqrt{1+\phi^2}\sqrt{6-6\phi+2\phi^2}\cos\theta$$ Now by using $\phi^2=\phi+1$ and $\phi=\frac{\sqrt5+1}{2}$ $$-2=2\sqrt{2+\phi}\sqrt{2-\phi}\cos\theta$$ $$-1=\sqrt{4-\phi^2}\cos\theta$$ $$\theta=\arccos\left(-\frac{1}{\sqrt{3-\phi}}\right)=\arccos\left(-\frac{\sqrt2}{\sqrt{5-\sqrt5}}\right)=\arccos\left(-\frac{\sqrt{5+\sqrt5}}{\sqrt{10}}\right)\approx 148.3^{\circ}$$
Hence, the obtuse angle between the face and the edge is $\alpha=270^{\circ}-\theta=121.7^{\circ}$.
This angle can be derived from the dihedral angle $\delta = \arccos (-1/\sqrt{5})$ of the dodecahedron using a vector method. (The dihedral angle $\delta$ is derived during construction of the dodecahedron - eg see this answer to How does this proof of the regular dodecahedron's existence fail?).
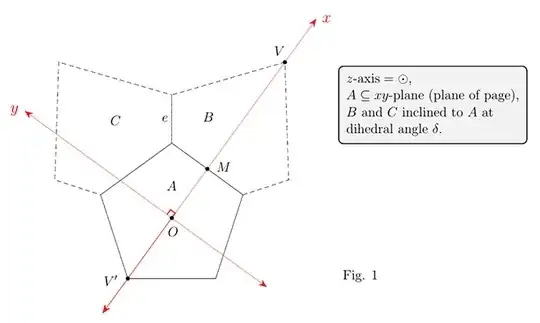
Consider a group of three adjacent pentagon faces as shown in Fig 1, in which pentagon $A$ is in the plane of the page, and $B$ and $C$ are tilted forwards to meet $A$ at the dihedral angle $\delta$. Each pentagon makes dihedral angle $\delta$ with the other two. The angle required is $\alpha$ between edge $e$ and the plane of pentagon $A$. If $\beta$ is the angle between the unit normal $\underline{\mathbf{u}}_A = \underline{\mathbf{k}}$ to $A$ and the unit vector $\underline{\mathbf{e}}$ along $e$, then $\alpha = \beta + 90$. Since edge $e$ is the intersection line of the planes $B$ and $C$, then if $\underline{\mathbf{u}}_B$ is a unit normal to $B$ and $\underline{\mathbf{u}}_C$ is a unit normal to $C$ then noting that the angle between $\underline{\mathbf{u}}_B$ and $\underline{\mathbf{u}}_C$ is the dihedral angle $\delta$, we have : $$\underline{\mathbf{e}} = \frac{1}{|\underline{\mathbf{u}}_B \times \underline{\mathbf{u}}_C|} \; (\underline{\mathbf{u}}_B \times \underline{\mathbf{u}}_C) = \frac{1}{\sin \delta} \; (\underline{\mathbf{u}}_B \times \underline{\mathbf{u}}_C). $$
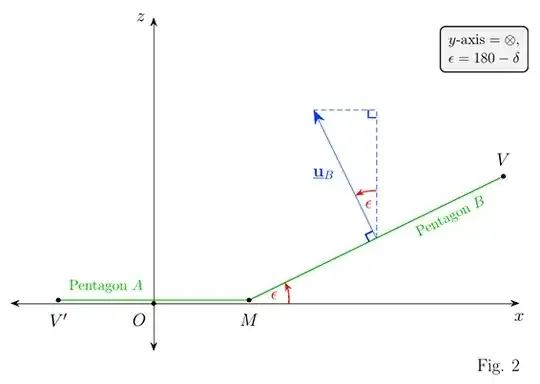
Setting up an $xyz$-axes system as shown in Figs 1 and 2 we have : \begin{eqnarray*} \underline{\mathbf{u}}_B & = & -\sin \epsilon\; \underline{\mathbf{i}} + \cos \epsilon\; \underline{\mathbf{k}} \\ \Rightarrow \hspace{1em} \underline{\mathbf{u}}_B & = & -\sin \delta\; \underline{\mathbf{i}} - \cos \delta\; \underline{\mathbf{k}} \end{eqnarray*}
Since pentagon $C$ is obtained from pentagon $B$ by rotating $B$ by $+72^\circ$ about the $z$-axis, we can obtain $\underline{\mathbf{u}}_C$ from $\underline{\mathbf{u}}_B$ by rotating $\underline{\mathbf{u}}_B$ by $72^\circ$ about the $z$-axis. (Note we are rotating vectors, which possess only direction and magnitude - they have no starting or ending point, in contrast to directed line segments, but can be 'placed' anywhere and will always point in the same direction). This rotation is a 2D rotation in the $xy$-plane and leaves the $\underline{\mathbf{k}}$ component unchanged, resulting in : $$ \underline{\mathbf{u}}_C = -\sin \delta \cos 72\; \underline{\mathbf{i}} - \sin \delta \sin 72\; \underline{\mathbf{j}} - \cos \delta\; \underline{\mathbf{k}} $$
Then : $$ \underline{\mathbf{u}}_B \times \underline{\mathbf{u}}_C = \sin^2 \delta \sin 72\; \underline{\mathbf{k}} -\sin \delta \cos \delta\; \underline{\mathbf{j}} + \sin \delta \cos \delta \cos 72\; \underline{\mathbf{j}} - \sin \delta \cos \delta \sin 72\; \underline{\mathbf{i}} $$
and so : $$ \cos \beta = \underline{\mathbf{k}} \cdot \underline{\mathbf{e}} = \frac{1}{\sin \delta} \; (\underline{\mathbf{u}}_B \times \underline{\mathbf{u}}_C) \cdot \underline{\mathbf{k}} = \sin \delta \sin 72 $$
and the desired angle $\alpha$ is given by : $$ \cos \alpha = \cos(\beta + 90) = -\sin \beta = -\sqrt{1 - \cos^2 \beta}. $$
The 18-72-90$^\circ$ triangle (which comes from the diagonal of a regular pentagon) tells us : $$ \sin 72 = \frac{\sqrt{4\Phi + 3}}{2\Phi} $$
where $\Phi$ is the golden ratio $\frac{1 + \sqrt5}{2}$.
The dihedral angle $\delta$ satisfies $\sin^2 \delta = 4/5$ so making use of the identity $\Phi^2 = \Phi + 1$ we now have: \begin{eqnarray*} \cos^2 \beta & = & \sin^2 \delta \sin^2 72 = \frac{4}{5} \cdot \frac{4\Phi + 3}{4\Phi^2} = \frac{4\Phi + 3}{5\Phi + 5} \\ \Rightarrow 1 - \cos^2 \beta & = & \frac{\Phi + 2}{5\Phi^2} \\ \Rightarrow \cos \alpha & = & -\frac{1}{\Phi \sqrt{5}} \sqrt{\Phi + 2} = -\frac{1}{\Phi \sqrt{5}} \sqrt{\frac{5 + \sqrt{5}}{2}} = -\frac{2}{1 + \sqrt{5}} \sqrt{\frac{5 + \sqrt{5}}{10}} \\ & = & -\frac{1}{2} \sqrt{\frac{(\sqrt{5} - 1)^2 (5 + \sqrt{5})}{10}} = -\frac{1}{2} \sqrt{\frac{(6 - 2\sqrt{5}) (5 + \sqrt{5})}{10}} \\ & = & -\frac{1}{2} \sqrt{\frac{20 - 4\sqrt{5}}{10}} = -\sqrt{\frac{5 - \sqrt{5}}{10}}. \end{eqnarray*}
Thus : $$ \alpha = \arccos \left\{ -\sqrt{\frac{5 - \sqrt{5}}{10}} \right\}. $$
