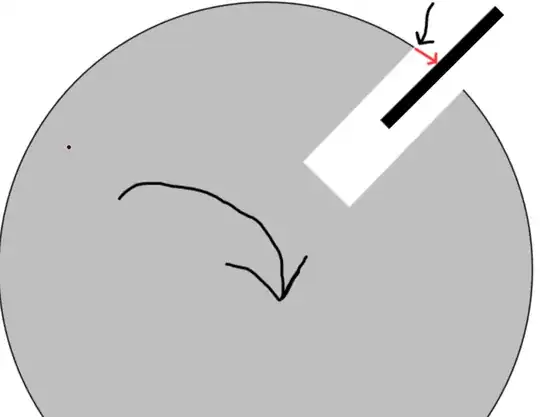
The circle's circumference is $c$ meters, and it rotates at a speed of $v$ RPM. The hole in the circle has a breadth of $l$ meters, and the pole (colored black) has a diameter of $d$ meters. The pole is in the center of the hole.
When will the circle's wall hit the pole?
Well, any point on the circle's circumference moves at a speed of $\frac{1}{60}vc \ \text{m}/\text s$. The red arrow is supposed to represent a straight line, going tangentially from the corner of the hole, to the surface of the pole. It has a length of $(l-d) \ \text m/2 $. From this, one might conclude that the wall and the pole will collide after the following amount of seconds:
$$\frac{(l-d) \ \text m/2 }{\frac{1}{60}vc \ \text{m}/\text s} =\frac{(l-d)60 \ \text s}{2vc} = \frac{(l-d)30 \ \text s}{vc} $$
But I reckon this is wrong, because the corner isn't moving in a straight line. Its path is curved, and that changes things. So, when will the wall hit the pole?