4

I tried to prove this: If $G$ is a $2$-connected graph with independence number $2$, then $G$ is Hamiltonian.

I was thinking to construct de hamiltonian cycle. We know that $G$ has independence number $2$ then exists two vertices that are not adyacent and using $2$-conectedness find two independents paths of the $2$ vertices. But I think that is very far-fetched, any help or hint will be welcome.

RobPratt
  • 50,938
TresTresUno
  • 224
  • Let $v_1,v_2$ be two non-adjacent vertices. The idea is to show that there is a path from $v_1$ to $v_2$ that visits every other vertex exactly once. –  Dec 25 '22 at 14:40

1 Answers1

3

Let $G$ be a $2$-connected graph with independence number $2$.

  1. The graph $G$ has at least three vertices and has cycles.

  2. Pick a cycle $C$ of maximal length and suppose there is a vertex $v$ outside this cycle.

  3. Since the graph is connected, we may assume that there are edges connecting $v$ with some vertices of cycle $C$.

  4. Let $A$ be the set of vertices of cycle $C$ adjacent to $v$.

Three cases are possible:

A) The set $A$ has two neighboring vertices in $C$.

B) The set $A$ has at least two elements and any two vertices from $A$ are not adjacent in $C$.

C) $|A|=1$.

In the first case $v$ can be included in a longer cycle than $C$ (see the left figure). Starting from the vertex $v$ we go first along the edge $vx$ and along the edge $yv$ we return.

If set A contains at least two vertices and $x,y\in A$, then $x$ and $y$ are not adjacent in $C$. But then $x_0$ and $y_1$ (see the middle figure) are adjacent in $G$ otherwise the set $v,x_0,y_1$ is independent. Now we get a cycle $vxx_1\ldots y_1x_0\ldots y_0yv$.

Let $|A|=1$ and $x\in A$. Let us remove the vertex $x$. The graph $G-x$ is by convention connected and hence there exists a path from $v$ to some vertex $C-x$ (see the right figure). As above, there exists edges $y_0y_1$ and $y'_0x_1$ and we have a cycle $vx\ldots y'_0x_1\ldots y_1y_0yz\ldots v$.

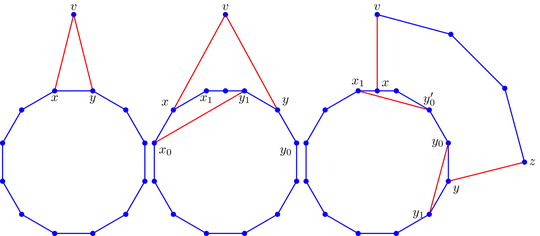
enter image description here

In all three cases we have a cycle longer than $C$, but this contradicts the choice of cycle $C$. It follows that the cycle $C$ is Hamiltonian.

Addition.(After 2 days)

In case (C) there are still a number of special cases: 1) $x$, $y$ are neighbors in the cycle $C$, 2) $x$, $y$ have a common neighbor in $C$.

kabenyuk
  • 12,395
  • I think your third image is wrong as it does not always lead to a longer cycle. However, if you fix an orientation for the cycle and pick the first vertices just before x and y (as in the second image, then you get a longer cycle. – caduk Dec 25 '22 at 10:15
  • @caduk: You are absolutely right, this is my mistake and I corrected it. Thank you very much. – kabenyuk Dec 25 '22 at 14:31