3

From http://mathinsight.org/dot_product:

$\LARGE{1. }$ "The dot product of $\mathbf{a}$ with unit vector $\mathbf{b}\backslash|\mathbf{b}|$ is defined to be the projection of $\mathbf{a}$ in the direction of $\mathbf{b}\backslash|\mathbf{b}|$, or the amount that $\mathbf{a}$ is pointing in the same direction as unit vector $\mathbf{b}\backslash|\mathbf{b}|$."

To obtain "the amount that $\mathbf{a}$ is pointing in the same direction as unit vector $\mathbf{b}\backslash|\mathbf{b}|$", why not define dot product as the orange vector instead of the red vector? The red arrows denote light rays perpendicular to $\mathbf{a}$; the orange arrows denote light rays perpendicular to $\mathbf{b}$.

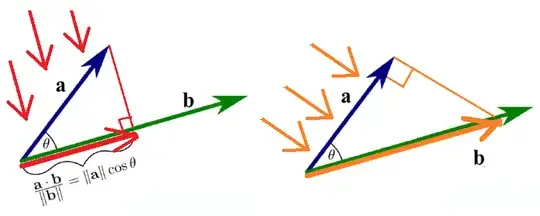
enter image description here

$\LARGE{2. } $ "We want a quantity that would be positive if the two vectors are pointing in similar directions, zero if they are perpendicular, and negative if the two vectors are pointing in nearly opposite directions. We will define the dot product between the vectors to capture these quantities."

Unfortunately, the above link does not explain: Why do we want these properties?

$\LARGE{3. }$ What is the motivation behind the symmetry of the dot products in $\mathbf{a}$ and $\mathbf{b}$ ?

I have referenced How to understand dot product is the angle's cosine? et Understanding Dot and Cross Product.

$\Large{\text{Supplement to Chris Culter's Answer:}}$

$\Large{\#1.1.}$ I'll let $\diamond$ denote the dot product as depicted in the orange, that which results from a projection induced by light rays perpendicular to $\mathbf{b}$.
How did you divine/foreknow that $\mathbf{x \diamond b} + \mathbf{y \diamond b} \neq \mathbf{(x + y) \diamond b ?}$
Thanks to your answer, I found a counterexample which I present underneath your Answer below.

Community
  • 1

2 Answers2

3

For #1, you could do that. But in the case where $\mathbf a$ and $\mathbf b$ are perpendicular, you would get infinity. You would also lose the identity $(\mathbf x + \mathbf y)\cdot \mathbf b = \mathbf x \cdot \mathbf b + \mathbf y \cdot \mathbf b$, because it's possible to have $(\mathbf x + \mathbf y)$ perpendicular to $\mathbf b$ even though neither neither $\mathbf x$ nor $\mathbf y$ is perpendicular to $\mathbf b$. It would be annoying to have to deal with infinities and to lose the distributive property; doing algebra with such quantities would get much harder!

For #2 and #3, I think it's best to compare the dot product with the cross product, since you're familiar with both.

  • The dot product is positive if the two vectors are pointing in similar directions, zero if they are perpendicular, and negative if the two vectors are pointing in nearly opposite directions. The dot product is also symmetric: $\mathbf a\cdot\mathbf b=\mathbf b\cdot\mathbf a$.

  • The cross product is zero if the two vectors are pointing in the exact same direction, nonzero if they are nearly perpendicular, and zero if the two vectors are pointing in opposite directions. The cross product is also antisymmetric: $\mathbf a\times\mathbf b=-\mathbf b\times\mathbf a$.

Both products are useful, but they have opposite properties! That proves that we don't have to demand any particular property of a product to get something useful. The definition itself isn't a logical argument. The dot product doesn't have to be defined the way it is. It's only later, when you see its applications, that it will be proven useful!

Chris Culter
  • 27,415
1

$\Large{\text{Annex to Chris Culter's Answer on August 5 :}}$

About $\#1$, I was trying to construct a natural and simple counterexample.
The colours refer to those in the picture below.
To ensure that $\mathbf{(x + y) \perp b}$, I wittingly define $\color{green}{\mathbf{b} = (1,0)}$ and $\mathbf{x+y} = (0,1)$.
Subsequently, for the purpose of $\mathbf{b} = (1,0)$, I see by inspection that the following works: $\color{red}{\mathbf{x} = (c, k)} \quad \& \quad \color{purple}{\mathbf{y} = (-c, 1 - k)} \; \forall c, k \in \mathbb{R}.$

For the purpose of sketching, pick $c = 1/2$ and $k = 1/3$ WLOG. I denote the orange IRregular dot product by $\diamond$. The picture below shows that $\mathbf{x \diamond b} \approx 0.8 $ while $\mathbf{y \diamond b} \approx -1.2 $. Therefore, $\mathbf{x \diamond b} + \mathbf{y \diamond b} \neq \mathbf{(x + y) \diamond b.}$

enter image description here

  • That works! I was thinking of a more trivial example: $\mathbf x = (\frac12,\frac12)$ and $\mathbf y = (-\frac12,\frac12)$. Then $\mathbf x \diamond \mathbf b = 1$ and $\mathbf y \diamond \mathbf b = -1$. Now, given my example, you might think that a modified form of the distributive law might hold that would combine $1$ and $-1$ to get $\infty$, maybe using harmonic addition. Your example has the nice property that there is no obvious relationship between $\mathbf x \diamond \mathbf b$ and $\mathbf y \diamond \mathbf b$, so it makes a stronger statement on how we've lost distributivity. – Chris Culter Aug 05 '13 at 05:59
  • Honestly, I don't remember. I think I noticed the perpendicular->infinity property first, just because I was curious what $\diamond$ would do in that case. Then I must have thought that it's hard to get to infinity with an operation that distributes over addition. – Chris Culter Aug 05 '13 at 06:26
  • One other consideration: distributivity of multiplication over addition is one of the defining properties of the geometric product, from which the dot product and the cross product can be obtained. I guess that means that anything that doesn't look like the dot product or cross product is unlikely to be distributive. I've never really studied geometric algebra, though; I've only seen bits and pieces of the topic. So don't take my word for it! – Chris Culter Aug 05 '13 at 06:28
  • @ChrisCulter: Many thanks for your supplementaries. Could you please explain why "it's hard to get to infinity with an operation that distributes over addition"? If I remember correctly, $\infty + \infty$ is not an indeterminate form and it $= \infty$. –  Aug 06 '13 at 02:04
  • Oh, I meant that the operation takes finite values for most inputs, and finite + finite = finite. So if the operation distributes over addition, then it basically has to have finite values everywhere. – Chris Culter Aug 06 '13 at 04:11
  • @ChrisCulter: Enormous thanks! I'll just summarise your meaning here. Under the IRregular dot product, $\diamond$, most inputs admit finite values. Also, perpendicularity $\implies \infty$. So if $\mathbf{(x + y) \perp b}$, then $\mathbf{(x + y) \diamond b} = \infty$. However, $\mathbf{x \diamond b} \quad & \quad \mathbf{y \diamond b} < \infty$. Since $\text{finite + finite} \neq \infty$, therefore distributivity fails. –  Aug 06 '13 at 07:39
  • Right, that's exactly what I meant! And by the way, we've spent so much time talking about the perpendicular case because it's convenient. Maybe we should stop to consider that $\diamond$ is probably non-distributive over addition for lots of other vectors too. In fact, it might be interesting to characterize the exact conditions under which $\mathbf{x \diamond b} + \mathbf{y \diamond b} = \mathbf{(x + y) \diamond b}$. Equality will hold if $\mathbf x$ and $\mathbf y$ are parallel, or if $\mathbf b = 0$. Are there other cases? I don't know! – Chris Culter Aug 06 '13 at 07:54