In 2013, when I was just a totally newbie recreational mathematician, I read about Levy's conjecture (i.e., Lemoine's conjecture, stating that all odd integers greater than 5 can be represented as the sum of an odd prime number and an even semiprime) and I came up with the idea that, by assuming Goldbach's strong conjecture as true, we would have easily deduced the following two conjectures (or at least one of them).
Conjecture 1: For every prime number $p_0 \geq 7$, there exists (at least) one pair of distinct primes ($p_1, p_2$) such that $p_0=2 \cdot p_1+p_2$.
Conjecture 2: $\forall n : n \in \mathbb{N}-\{0,1,2,3,4,5,6,7\}$, there exists (at least) a couple of odd primes, $p_1 \neq p_2$, such that $2 \cdot n+1=2 \cdot p_1+p_2$.
About Conjecture 1, the number of ways such that $p_0=2 \cdot p_1+p_2$ seems to increase almost linearly (see Figure below) and a brute force test has been performed up to $746562601=2 \cdot 7+746562587$, confirming the statement for every $p_0 \leq 746562601$.
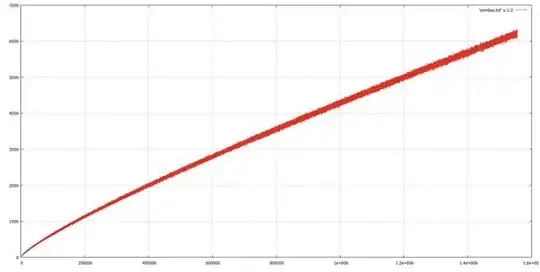 Number of ways to write $p_0$ as $2 \cdot p_1+p_2$
Number of ways to write $p_0$ as $2 \cdot p_1+p_2$
Any chances to prove the above by taking the strong Goldbach Conjecture as true?