2

Let $A$ be a commutative ring and $S$ a multiplicatively closed system. I am trying to see that if $\alpha \colon N_1 \rightarrow N_2$ is an $A$-linear map of $A$-modules which are in fact $S^{-1}A$-modules, then $\alpha$ is in fact $S^{-1}A$-linear. I want to do this just using the universal property of the localisation. Is this possible?

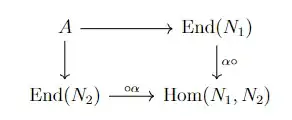
My attempt is as follows: $\alpha$ being $A$-linear just means that we have a commuting diagram A \rar End(N_1) \rar Hom(N_1,N_2) = A \rar End(N_2) \rar Hom(N_1,N_2)

Now by the universal property, $A \rightarrow S^{-1}A$ is initial among ring maps $A \rightarrow B$ sending $S$ to invertibles. Now since $N_1$, $N_2$ are even $S^{-1}A$ modules, $A \rightarrow \mathrm{End}(N_1)$ and $A \rightarrow \mathrm{End}(N_2)$ are two maps sending $S$ to invertibles. Hence, we have a larger diagram which I want to show is commutative:

enter image description here

The problem is, how can I conclude from this that $$ S^{-1}A \rightarrow \mathrm{End}(N_1) \rightarrow \mathrm{Hom}(N_1, N_2) = S^{-1}A \rightarrow \mathrm{End}(N_2) \rightarrow \mathrm{Hom}(N_1, N_2) \,. $$ One would be tempted to use the uniqueness of the map from $S^{-1}A$ to any ring $B$ where $A \rightarrow B$ sends $S$ to invertibles. The problem is that $\mathrm{Hom}(N_1, N_2)$ is not a ring!

Even so, I haven't used uniqueness yet, but I don't see how.

Jendrik Stelzner
  • 17,081
rosecabbage
  • 1,883
  • I don't think this has to be true. – Randall Nov 23 '22 at 13:48
  • If $A$ is commutative, it is definitely true @Randall. See that $$b\alpha(\frac{a}{b}n) = \alpha(b\frac{a}{b}n) = \alpha(an)=a\alpha(n) = b\frac{a}{b}\alpha(n)$$ for $a\in A$, $b\in S$, and $n\in N_1$. Then, if $b$ is not a zero-divisor, the zero rule gives the desired result. If $b$ is a zero-divisor, $S$ contains $0$, and so everything is trivial. I don't know how to formulate this in terms of universal properties though. – SomeCallMeTim Nov 23 '22 at 14:24
  • Oh yes, I meant that $A$ is commutative to start with, sorry. I can see it's trivial using the explicit construction of the localization, but yes, I'm wondering if there's a way to prove it using the universal property. – rosecabbage Nov 23 '22 at 14:28
  • 1
    You should consider the localization on modules, not on rings. – Claudius Nov 23 '22 at 14:54
  • Note that an analogous statement holds for any epimorohism of rings $R \to T$ – Lukas Heger Nov 23 '22 at 15:58
  • 1
    See https://math.stackexchange.com/q/2798579/348926 – Lukas Heger Nov 23 '22 at 15:59
  • @Claudius Do you mean I should show that $A \rightarrow S^{-1}A$ is both the localization of $A$ as a ring and as an $A$-module, and then use the universal property of $S^{-1}A$ as the localization of the $A$-module $A$ to deduce what I want, taking into account the fact that $Hom(N_1, N_2)$ is an $A$-module? – rosecabbage Nov 23 '22 at 16:29
  • 1
    Not quite. Rather, the localization $M\mapsto S^{-1}M$ is left adjoint to the restriction of scalars, say $F$, along $A\to S^{-1}A$. You ask that $F$ is fully faithful and this is equivalent to showing that the counit of the adjunction $S^{-1}F(M) \to M$ is an isomorphism of $S^{-1}A$-modules. And this can be checked using the universal property. – Claudius Nov 23 '22 at 16:44

1 Answers1

1

Let us abbreviate $\mathrm{Hom}_ℤ$ and $\mathrm{End}_ℤ$ as $\mathrm{Hom}$ and $\mathrm{End}$ respectively.

Framework

Let us first consider two abelian groups $M$ and $N$. The abelian group $\mathrm{Hom}(M, N)$ becomes a left $\mathrm{End}(N)$-module via postcomposition and a right $\mathrm{End}(M)$-module via precomposition. For a given element $f$ of $\mathrm{Hom}(M, N)$ we can consider the set $$ E_f := \{ (h, k) ∈ \mathrm{End}(M) × \mathrm{End}(N) \mid h f = f k \} \,. $$ This set is a subring of $\mathrm{End}(M) × \mathrm{End}(N)$. It is also closed under invertibility, in the following sense: whenever $(h, g)$ is an element of $E_f$ that is invertible in $\mathrm{End}(M) × \mathrm{End}(N)$, its inverse $(h, k)^{-1} = (h^{-1}, k^{-1})$ is again contained in $E_f$.

Observation

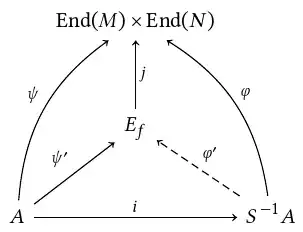
The ring $E_f$ helps us understand module structures on $M$ and $N$ for which $f$ is a homomorphism.

Let $B$ be a ring. A $B$-module structure on $M$ is the same a homomorphism of rings from $B$ to $\mathrm{End}(M)$. Simultaneous $B$-module structures on $M$ and $N$ are therefore the same as a pair $(φ_1, φ_2)$ of homomorphisms of rings $φ_1 \colon B \to \mathrm{End}(M)$ and $φ_2 \colon B \to \mathrm{End}(N)$. Such a pair of homomorphisms is the same as a single homomorphism $φ \colon B \to \mathrm{End}(M) × \mathrm{End}(N)$ (whose components are given by $φ_1$ and $φ_2$).

The map $f$ is a homomorphism of $B$-modules if and only if the image of $φ$ is contained in the subring $E_f$ of $\mathrm{End}(M) × \mathrm{End}(N)$. In other words, if and only if there exists a homomorphism of rings $φ' \colon B \to E_f$ such that $φ = j ∘ φ'$, where $j$ is the inclusion map from $E_f$ to $\mathrm{End}(M) × \mathrm{End}(N)$.

The problem at hand

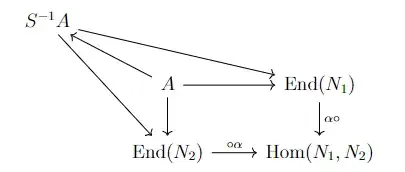
enter image description here

Let us now consider the original problem: $M$ and $N$ are not just abelian groups, but $S^{-1} A$-modules. These simultaneous $S^{-1} A$-module structures correspond to a homomorphism of rings $φ \colon S^{-1} A \to \mathrm{End}(M) × \mathrm{End}(N)$. We can regard $M$ and $N$ as $A$-modules by restriction, and these simultaneous $A$-module structures correspond to a homomorphism of rings $ψ \colon A \to \mathrm{End} × \mathrm{End}(N)$. The homomorphism $ψ$ is just the restriction of $φ$ to $A$. More precisely, $ψ = φ ∘ i$ where $i$ is the canonical homomorphism from $A$ to $S^{-1} A$.

Suppose that $f$ is not only additive, but also $A$-linear. This means that the image of $ψ$ is contained in $E_f$. In other words, there exists a homomorphism of rings $ψ'$ from $A$ to $E_f$ with $φ' = j ∘ ψ'$.

For every element $s$ of $S$ the element $ψ'(s)$ of $E_f$ is invertible in $\mathrm{End}(M) × \mathrm{End}(N)$, because $s / 1$ is invertible in $S^{-1} A$ and $ψ'(s) = ψ(s) = φ(s / 1)$. We have seen that $E_f$ is closed under invertibility, so it follows that $ψ'(s)$ is already invertible in $E_f$. It now follows from the universal property of the localization $S^{-1} A$ that there exists a unique homomorphism of rings $φ'$ from $S^{-1} A$ to $E_f$ with $φ' ∘ i = ψ'$. We have $j ∘ φ' ∘ i = j ∘ ψ' = ψ = φ ∘ i$ and therefore $j ∘ φ' = φ$. In other word, $φ'$ is the restriction of $φ$ to a homomorphism of rings from $S^{-1} A$ to $E_f$. The existence of this restriction tells us that $f$ is $S^{-1} A$-linear.

Jendrik Stelzner
  • 17,081