1

I have been having a lot of trouble trying to solve this problem, I have tried to work with some numbers, but I find many ways to do it, I do not arrive at anything concrete.

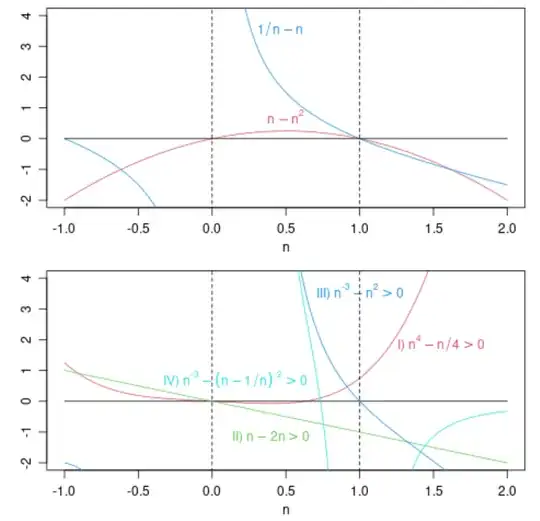
According to the information given in the attached number line, which of the following statements is (are) true? $$I) n^4 > \frac{n}{4}$$ $$II) 2n<n$$ $$III)n^{(-3)} > n^2$$ $$IV) (n - \frac{1}{n})^{(-2)} <n^{(-3)}$$

enter image description here

Original at https://i.sstatic.net/9LMxT.png

David G. Stork
  • 30,409
Pamela
  • 31
  • 1
    Okay, we know that $n^2 < n < \frac 1n$ that's pretty unusual. Can you deduce what that might mean? – fleablood Nov 19 '22 at 22:55
  • 1
    Remember if $a< b$ and $c > 0$ then $ac < bc$. And if $0<a$ and $c > 1$ then $a < ac < ac^2 < ac^3 < .........$. And if $0< a < b$ then $a^2 =a\cdot b < a\cdot b =b^2$ and so on. – fleablood Nov 19 '22 at 23:07
  • 1
    Note the only time $2n < n$ is when $n < 0$. Is $n< 0$? – fleablood Nov 19 '22 at 23:09
  • I'm blocked sorry – Pamela Nov 19 '22 at 23:10
  • 1
    Think it out. $x^2 \ge 0$. If $0 < x < 1$ then $x^2 < x$ but if $x>1$ then $x < x^2$. Also if $x > 1$ then $0 < \frac 1x < 1$ and vice versa, if $0 < x < 1$ then $\frac 1x > 1$. So you have $n^2 < n < n^{-1}$. That tells us something very important. That one thing will make most of those straightforward. – fleablood Nov 19 '22 at 23:16
  • Thank you for answering, no matter how much I analyze what you have written to me, I lose. Could you answer for each option please? example i) is true because ....or is false because.... – Pamela Nov 19 '22 at 23:45
  • I think I'm dizzy thinking that it can't be any real except zero – Pamela Nov 19 '22 at 23:47
  • 1
    Oh, it can't be $0$. If it were $0$ then $n^2 = n$ and $n^{-1}$ would be undefined. But it could be $n=\frac 12$. If $n = \frac 12$ then $n^2 = \frac 14; n =\frac 12;$ and $n^{-1} = 2$ and we would have $n^2 < n < n^{-1}$. But that's only one possible value $n$ can be. What other values can we have? – fleablood Nov 20 '22 at 00:06

3 Answers3

3

I'll keep the letter $n$ although using it to denote a real number is utterly unsatisfying. The image tells you that $$n^2<n<\frac{1}{n}.$$ The first inequality is attained iff $0<n<1$ (¿why?). So the second inequality tells you nothing.

At first glance, (II) is wrong. Now, you can plug some specific values of $n$ (e. g. $n=1/2$) in the remaining inequalities to (possibly) get rid of the wrong ones. Spoiler: all of them are wrong.

moqui
  • 1,421
  • 7
  • 21
  • 3
    I'd say I and IV are not true, but I wouldn't say they are "wrong". They can be true for some but not all acceptable values of $n$. Wheres II and III are false for all acceptable values of $n$. – fleablood Nov 20 '22 at 00:01
2

Okay.... we have $n^2 < n < n^{-1}$.

Now $n^2 \ge 0$ so we have $0 \le n^2 < n < n^{-1}$ so $n > 0$.

Since $n > 0$ we can multiply or divide by $n$ and maintain the inequality.

If we multiply all by $n$ we get $n^2\cdot n < n\cdot n < n^{-1}\cdot n$ or $n^3 < n^2 < 1$ and if we divide all by $n$ we get $\frac {n^2}n < \frac nn < \frac {n^{-1}}n$ or $n < 1 < n^{-2}$.

So we have $0 < n < 1$.

I'll leave it to you to do the rest....

Well, no... I'll do II) $n> 0$ so $n+n > n+0$ so $2n > n$. So II) which say $2n < n$ is always false.

We could also have done that since $n> 0$ then $2n < n$ is true only if $\frac {2n}n < \frac nn$ or if $2 < 1$. Since $2 > 1$ it can not be true.

fleablood
  • 130,341
1

The information from the numberline gives two conditions

$$\begin{array}{rcl} n-n^2 &>&0 \\ 1/n-n&>&0 \end{array}$$

These conditions are satisfied when $0<n<1$

Then you need to check the four statements

$$\begin{array}{rrcl} \text{I)}& n^4-n/4 &>&0 \\ \text{II)}& n-2n &>&0 \\ \text{III)}& n^{-3}-n^2 &>&0 \\ \text{IV)}& n^{-3}-(n-1/n)^{-2} &>&0 \\ \end{array}$$

The image below is a spoiler which shows that statement III is true, statement II is false, and statements I and IV can not be determined with the information. You can proof it algebraically for all those four cases. For example case II is simple $n-2n = -n>0$ or $n<0$ which is false when $0<n<1$.

graphical example

Sextus Empiricus
  • 1,320
  • 7
  • 19