What is the topological space with fundamental group isomorphic to this presentation $\langle a,b \mid a^2=b^2\rangle$?

Question

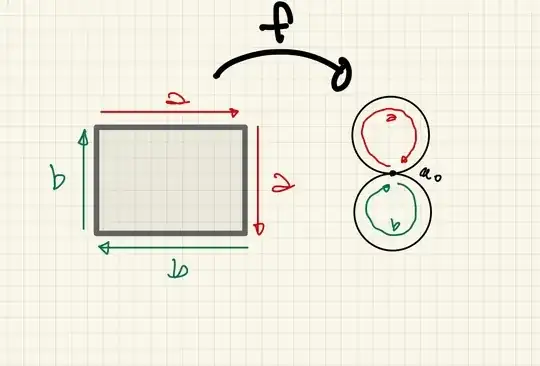
In this answer, it talks about how you can create a topological space with the following fundamental group: $$\langle a,b \mid a^2=b^2\rangle$$ The answer does this by creating a topological space consisting of two unit circles that are connected to the unit cylinder by the path that goes around the circles twice, and then shows that that is the space with this fundamental group by proving that the space is homeomorphic to the Klein Bottle and therefore has fundamental group isomorphic to that of the Klein Bottle.

How do you show that the presentation is isomorphic to the fundamental group of that topological space, i.e. $$\pi_1 (X) \cong \langle a,b \mid a^2=b^2\rangle$$ where $$X=\mathbb{S}^1 \sqcup \mathbb{S}^1 \times [0,1] \sqcup \mathbb{S}^1/\sim $$ where the quotient takes $\mathbb{S}^1 \times 0$ to the path that goes twice around the first copy of the circle and $\mathbb{S}^1 \times 1$ to the path that goes twice around the second copy of the circle, without reference to the fundamental group of the Klein Bottle?

Answer 1

Start with a point $x_0$, and attach to it two copies of $[0,1]$ so that the four endpoints are identified with $x_0$. It follows from vK's theorem that the $\pi_1$ of the space $X$ we got in this way — a wedge of two circles, we call it — is the free group on two generators. Those generators can be chosen to be the curves $a:[0,1]\to X$ and $b:[0,1]\to X$ that go around each of the two circles, starting and ending at $x_0$. This is a consequence of the description of $\pi_1(X,x_0)$ that gives us vK's theorem, in fact, since $a$ and $b$ are generators of the $\pi_1$ of the spaces we glued.

Now let $Q=[0,1]\times[0,1]$ be a square. We want to describe a map $f:\partial Q\to X$: the boundary of $Q$ is the union of four segments, glued at the vertices, and we can let $f$ "act" as the curve $a$ on two of themm and as curve $b$ on the other two, as in the following diagram:

Explicitly, this means that if $(x,y)$ is a point in $\partial Q$, then $$f(x,y)=\begin{cases} a(x) & \text{if $y=1$;} \\ a(1-y) & \text{if $x=1$;} \\ b(1-x) & \text{if $y=0$;} \\ b(y) & \text{if $x=0$.} \end{cases} $$

Now let $Y$ be the result of gluing the square $Q$ to the space $X$ by identifying points in $\partial Q$ to their images through the map $f$. A standard application of vK's theorem tells you that the fundamental group of $Y$ based at $x_0$ is the quotient of the $\pi$ of $X$ modulo the normal subgroup generated by the homotopy class of the curve in $X$ that one gets by going around the boundary of $Q$ once, which is $aabb$.

In other words, $$\pi_1(Y,x_0) = \langle a,b\mid aabb\rangle,$$ and this is the group you wanted.

Answer 2

This is just a fantasy, not a solution. There will be some gaps. I hope you do downvote this as usual.

Let $\tilde{X}=\Bbb{R}\sqcup\Bbb{R}\times I\sqcup\Bbb{R}/\sim$ be the covering space of $X$ which is obtained by gluing $\frac{1}{2}$ times of the first copy of $\Bbb{R}$ to $\Bbb{R}\times{0}$ and $\frac{1}{2}$ times of the second copy of $\Bbb{R}$ to $\Bbb{R}\times{1}$. Let $\pi:\tilde{X}\times X$ be the quotient map.

Let $a: S^1\rightarrow X$ be the map which sends $S^1$ identically to the first copy of $S^1$ in $X$ and similarly $b: S^1\rightarrow X$ be the map which sends $S^1$ identically to the second copy of $S^1$ in $X$.

Then we can lift $a$ to $\tilde{a}: S^1\rightarrow\tilde{X}$ uniquely so that $\tilde{a}(0)=(0,0)$ and $\tilde{a}(1)=(\frac{1}{2},0)$. So, $a$ is non-trivial. Similarly, we can lift $b$ to $\tilde{a}: S^1\rightarrow\tilde{X}$ so that $\tilde{b}(0)=(0,1)$ and $\tilde{b}(1)=(\frac{1}{2},1)$. So, $b$ is non-trivial. (We need some theorems from covering spaces here.)

Let $x:I\rightarrow \tilde{X}$ such that $x(t)=(t,0)$ and $y:I\rightarrow \tilde{X}$ such that $y(t)=(t,1)$. Then $\pi_{*}(x)=a^2$ and $\pi_{*}(y)=b^2$. Now we can slide paths in$\tilde{X}$ so that $x\simeq y$ and hence we get homotopy $a^2 \simeq b^2$ of the loops in $X$.