As have been mentioned in the comments, the equation defines a plane. To 'solve' the equation, maybe you mean, what values for $x,$y provide a desired value of $z$.
I would assume that this problem qualifies to be a "Diophantine Equation".
A rigorous technique to solve such a problem, is discussed with an example in the answer of the user: robjohn in:Extended Euclidean Algorithm.
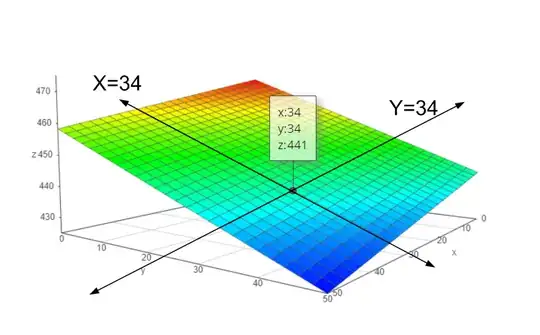
Assuming that you are not interested in deep theory, you can get a 'solution' either by a simple computer program with nested loops or a plot of the function in the form $z=..."$, such as the one below. Depending on the plotting tool, you can get more information about any point in the plane by a mouse click. Each positive-valued pair of $x$ and $y$ on the plane is a 'solution'. Note that the shown picture does not represent all solutions, since it is plotted in a specific range. Graphing could answer some questions one can't easily get a closed-form for sometimes.
The plot below is made for $z=(2850-2x-4y)/6$
If you have more information, for example $x+y<= 30$ for $Z=441$, in this case you could further limit the number of points that satisfies the relationship.
It may be interesting to know that there is a branch in Mathematics called "Integer Linear Programming" that deals with finding extreme value for such relationships.
The tool used is:3-D Surface Plotter

cnt=0;forstep(z6=6,2850,6,forstep(y4=4,2850-z6,4,x2=(2850-z6-y4); if(x2<2,next()); if(x2 % 2,next()); cnt++));cnt– Gottfried Helms Nov 12 '22 at 12:10