The result of a standard form line equation

Question

If we substituted a point in the standard form equation, what the resulting number indicates?

For example:

We have the line: $$3x + 6y + 12 = 0$$

And we have the point $I(1,2)$

Substituting I in the line equation:

$$3(1) + 6(2) + 12 = 0$$

$$=> 27 = 0$$

Does this only means that the point does not belong to the line?

And what the $27$ indicates in this example?

(I know that if the resulted number is positive that means that the point is above the line and if it is negative the point is below the line). But my question is that if the number $27$ indicates something, apart from the sign

Answer 1

A point $P(a,b)$ is in the line $3x+6y+12=0$ if, and only if, $$3a+6b+12=0.$$ In this case since the LHS is just $3(1)+6(2)+12=27$ and the RHS is just $0$, so $LHS\not=RHS$ and it follows that the point $I(1,2)$ is not the line $3x+6y+12=0$.

Answer 2

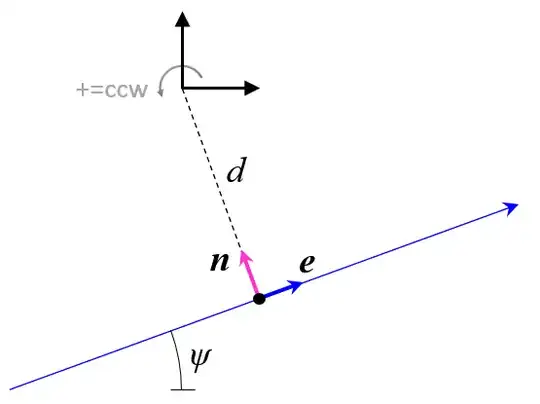
General reference : https://en.wikipedia.org/wiki/Distance_from_a_point_to_a_line

Here is an answer that (I think so) adresses the question.

Let us write the equation of line L under the form

$$f(x,y)=0 \ \text{where} \ f(x,y)=ax+by+c$$

Plugging the coordinates $x=x_0, y=y_0$ of point I in it,

Result: The value of $f(x_0,y_0)$ is proportional to the oriented (shortest) distance of I to the straight line L, with a constant proportionality factor.

Otherwise said : there exist a constant $K$ such that:

$$f(x_0,y_0) = K \times \ \text{dist}((x_0,y_0), L) \tag{1}$$

What is meant by "signed distance" ? Its absolute value is the ordinary distance ; its sign indicates the side of the straight line where point $I(x_0,y_0)$ is situated.

Example : In the graphical representation, $f(x,y)=x+y-1$ (in red), the values of $f(x_0,y_0)$ for different points are given. You can check that they are all proportional to the distance, with a proportionality factor equal to $\sqrt{2}=\sqrt{a^2+b^2}=sqrt{1^2+1^2}$. This graphical representation features different "level lines" for function $f(x,y)=c$ :

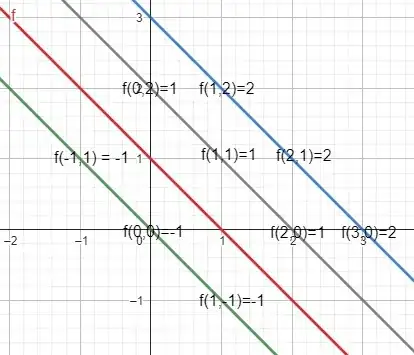
Example : point $I(1,1)$ is such that

$$f(1,1)=1 \tag{2}$$

The constant $K$ being $\sqrt{2}$, formula (1) gives:

$$dist(I,L)=1/\sqrt{2}=\sqrt{2}/2$$

which is indeed half the length of the diagonal of a square with side 1.

Remark: there is a re-interpretation using a generalization of (2) by considering equation $z=f(x,y)$, which is the equation of a slant plane P intersecting horizontal plane along line L. The level lines mentionned above are plainly the projection onto horizontal $x-y$ plane of level lines of this plane P. I don't go further on because I know by experience that invoking 3D geometry for understanding 2D concepts is often very fruitful, but can also be confusing for learners.

Answer 3

Take the general form of the line $A x + B y + C = 0$ and calculate the perpendicular distance to an arbitrary point $(x,y)$

$$ {\rm dist} = \frac{| Ax +By+ C |}{\sqrt{A^2+B^2}}$$

You are asking about the numerator. If you normalize the coefficients of the equation such that $A^2+B^2 = 1$, then $f = |A x + B y + C| $ is just the distance to that point.

If $A x + B y + C =0 $ is zero then the point belongs on the line.

• The signed distance to a point is $$ {\rm dist} = \frac{ Ax +By+ C }{\sqrt{A^2+B^2}}$$ the sign is negative if the point is closer to the origin from the line, and positive of the point is beyond the line.

• The normal vector of the line is $$\boldsymbol{n} = \frac{1}{\sqrt{A^2+B^2}} \pmatrix{-B \\ A}$$ The normal vector is defined here as pointing towards the origin

You can parameterize the equation of the line using its direction angle $\psi$ and distance from origin $d$ as

$$ (\sin \psi) x + (-\cos \psi) y + (-d) = 0 $$

where $A=-\sin \psi$, $B=\cos \psi$, and $C=-d$