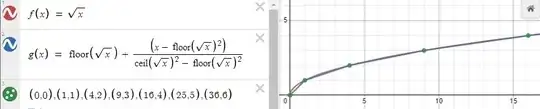
If you connect the lattice points of $f(x) = \sqrt{x}$ together through secant lines, you create a function $ g(x) = \left\lfloor \sqrt{x} \right\rfloor + \frac{x - \left\lfloor \sqrt{x} \right\rfloor^2}{\left\lceil \sqrt{x} \right\rceil^2 - \left \lfloor \sqrt{x} \right \rfloor^2}$.
I was attempting to find the area between f(x) and g(x) for different ranges given by the lattice points that they shared ((1,1), (4,2), (9,3), etc), and then using those as boundaries (upper boundary being $x^2$, lower boundary being $(x - 1)^2$), which be: $$\int_{(x - 1)^{2}}^{x^{2}} (f(x) - g(x))dx $$ Using desmos, I figured that this value is 1/6 for all natural numbers (it changes for other numbers, but they would not matter because x represents different ranges, and having a non-integer number wouldn't make sense there). Is that a coincidence, or is there more to it? Thanks in advance!