Approximate inverse of $k=\frac{\log (1-t)}{\log (t)}$

Question

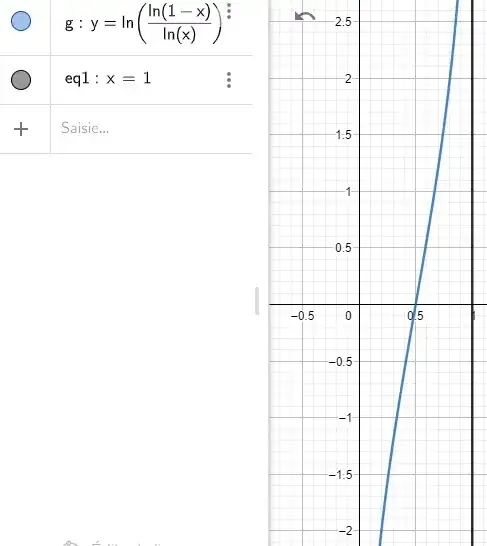
Trying to answer this question where we look for the solution of $$\large\color{red}{t^k+t=1} \qquad \qquad \text{with} \qquad \color{red}{0<k<1}$$ which is more or less the function Lambert considered.

In my update, I rewrote it as $$\large\color{blue}{k=\frac{\log (1-t)}{\log (t)}}$$

The plot of $t$ as a function $k$ is not very nice but my surprise came from the plot of $t$ as a function of $\log(k)$ which is extremely close to a logistic function.

I came very quickly to the approximate result $$\large\color{blue}{t\sim\frac 1 {1+k^{-\log_2 (\phi )}}}$$ ($\phi$ being the golden ratio). This reproduces exactly the value of $t$ for $k=\frac 12$; at this point, the slope is in a relative error of $0.3$%.

This surprising value being used as the $t_0$ of Newton method, some results

$$\left( \begin{array}{cccc} k & t_0 & t_1 & \text{solution} \\ 0.05 & 0.11107938 & 0.10607326 & 0.10610459 \\ 0.10 & 0.16818422 & 0.16491137 & 0.16492096 \\ 0.15 & 0.21130781 & 0.20917626 & 0.20917956 \\ 0.20 & 0.24650516 & 0.24512115 & 0.24512233 \\ 0.25 & 0.27639320 & 0.27550762 & 0.27550804 \\ 0.30 & 0.30240988 & 0.30186067 & 0.30186067 \\ 0.35 & 0.32545141 & 0.32513010 & 0.32513010 \\ 0.40 & 0.34612246 & 0.34595481 & 0.34595481 \\ 0.45 & 0.36485403 & 0.36478837 & 0.36478837 \\ 0.50 & 0.38196601 & 0.38196601 & 0.38196601 \\ 0.55 & 0.39770340 & 0.39774335 & 0.39774335 \\ 0.60 & 0.41225852 & 0.41232020 & 0.41232020 \\ 0.65 & 0.42578544 & 0.42585602 & 0.42585602 \\ 0.70 & 0.43840971 & 0.43848026 & 0.43848026 \\ 0.75 & 0.45023507 & 0.45029952 & 0.45029952 \\ 0.80 & 0.46134837 & 0.46140274 & 0.46140274 \\ 0.85 & 0.47182302 & 0.47186491 & 0.47186491 \\ 0.90 & 0.48172173 & 0.48174985 & 0.48174985 \\ 0.95 & 0.49109845 & 0.49111241 & 0.49111241 \\ \end{array} \right)$$

To give an idea, I considered as a measure $$\Phi_n=\int_0^1 \Bigg[k-\frac{\log (1-t_n)}{\log (t_n)}\Bigg]^2\,dk$$ $$\Phi_0=2.157 \times 10^{-6}\qquad \Phi_1=6.282 \times 10^{-11}\qquad \Phi_2=4.007 \times 10^{-18}$$

Edit

After @Jam's answer, I minimized $$\Psi(a)=\int_0^1 \Bigg[k-\frac{\log \left(1+k^a\right)}{\log \left(1+k^{-a}\right)} \Bigg]^2\,dk$$ The result is $$a_{\text{min}}=0.69603517 \quad \implies \quad \Psi(a_{\text{min}})=1.668 \times 10^{-6}$$

For this number, the $ISC$ proposes the amazing $$a_{\text{min}}\sim \frac{\sqrt[2]{2}\,\, \sqrt[3]{3}-9}{10} $$

Could this be even partly justified ?

Answer 1

From $t^k+t=1$, we indeed have, as you derived, $\displaystyle k=\frac{\ln\left(1-t\right)}{\ln t}$. And you claim that the graph of $t$ against $\ln k$ appears to be approximately a logistic function in $\ln k$, given by $\displaystyle t=\frac{1}{1+e^{-a\ln k}}=\frac1{1+k^{-a}}$ for some constant $a\approx 0.693$. However, instead of your $a=\log_{2}\left(\frac{\sqrt{5}+1}{2}\right)=0.694$, I find $a=\ln 2=0.693$.

We justify the claim as follows, by proving, in particular, that the implicit function $\displaystyle e^{x}=\frac{\ln\left(1-y\right)}{\ln y}$, in which $x$ corresponds to $\ln k$ and $y$ to $t$, has a derivative that is approximately quadratic in $y$, which implies the desired logistic approximation.

Through implicit differentiation and the chain and quotient rules, we have $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}=\frac{-1}{u\left(1-y\right)+u\left(y\right)}$, where $u(x)=1/({x\ln x})$. Then, $ \frac{\mathrm{d}y}{\mathrm{d}x}$ is, with respect to $y$, concave down (inverse U-shaped) and symmetric about $x=0.5$, with zeros at $x=0$ and $1$ and a maximum of $\ln (2) / 4$. If we then fit a quadratic in $y$ to $ \frac{\mathrm{d}y}{\mathrm{d}x}$ with roots at $0,1$ also and an identical maximum, it will be exactly equal to $ \frac{\mathrm{d}y}{\mathrm{d}x}$ at $0$, $0.5$, and $1$, and, by continuity, have an error that is concave and bounded (and, in principle, small) on each of the two intervals between those values. Numerically, we indeed find that the absolute error is at most $4.82\times10^{-3}$.

This gives the approximation $ \frac{\mathrm{d}y}{\mathrm{d}x}\approx \ln 2\, y (1-y)$, which is a differential equation with the logistic function $\displaystyle y=\frac{1}{1+C\,2^{-x}}$ as its solution, where we see from the initial value $y(0)=0.5$ that $C=1$. And therefore, $\displaystyle t\approx \frac1{1+k^{-\ln 2}}$.

Answer 2

I do not have much experience with these curves. I tried change of variables. But for me, $x$ and $y$ complicated the equations.

1. If $t^k+t=1$ fits $k^ct+t=1$ then $t^{k-1}$ fits $k^c$. At $(k,t)=(2,\phi^{-1})$ we have $c=-\frac{\ln\phi}{\ln 2}$.

2. By implicit differentiation, $\frac{dt}{dk}=-\frac{t^k\ln t}{kt^{k-1}+1}$ fits $\frac{dt}{dk}=-\frac{ck^{c-1}}{(1+k^c)^2}$. Then, I somehow found that $c$ fits $\frac{k\ln t}{k(1-t)+t}$ and at $(k,t)=(2,\phi^{-1})$, we have $$c=-\frac{2\phi^2\ln\phi}{\phi +2}\approx -0.696416$$

Answer 3

There is an analytical solution using a new special function called

$W_q(z)$ or Lambert-Tsallis function. This function is defined as a solution of $ X\cdot (1 + (1-q)\cdot X)^\frac{1}{1-q} = z$.

For sake of simplicity I like to call it $W_{"r"}(z)$ Defined as solution of the polynomy

$ X\cdot \bigg(1 + \frac{X}{r}\bigg)^r = z$, and $r=\frac{1}{1-q}$

So, only for a detail of nomenclature, after a few manipulation one can analitically find

$ t = \bigg(\frac{W_{"r"}(r)}{r}\bigg) ^\frac{1}{r\cdot k}$ (1)

and $r=\frac{1-k}{k}$

When $k=0.5$ one has $r=1$. However, $W_{"1"}(1)=\phi=0.618033248239453$ or $-1.618034622558085$. Only the positive value is considered. Thus, substituting, one would take

$ t = \bigg(\frac{\phi}{1}\bigg) ^2 = 0.381965095929409$ that corresponds to the values found at table. The analytical results using $W_q(z)$ is show in the following tables for $t$ using the same previously data

t	k
0.106105111882033	0.05
0.164920356980167	0.10
0.209179436174934	0.15
0.245122552355033	0.20
0.275507532000750	0.25
0.301861318986113	0.30
0.325130035349145	0.35
0.345954813133744	0.40
0.364788831763960	0.45
0.381966555040667	0.50
0.397742867431469	0.55
0.412320670850846	0.60
0.425855828574802	0.65
0.438480356363474	0.70
0.450299821476583	0.75
0.461403048715524	0.80
0.471864671170827	0.85
0.481750909739635	0.90
0.491111506254522	0.95

Answer 4

Working directly with

\begin{equation} t^{k}+t-1=0 \end{equation}

Transforming the equation with the change of variable $t\rightarrow1-1/z$ and multiplying by z, we obtain the equation

\begin{equation} z\left(1-\frac{1}{z}\right)^{k}-1=0 \end{equation}

Defining the function $f(z)=z\left(1-\frac{1}{z}\right)^{k}-1$ and applying the Burniston-Siewert method to solve transcendental equations to this equation we obtain

\begin{equation} t=1-\frac{1}{k+1-m} \end{equation}

where

\begin{equation} m=\frac{1}{\pi}{\displaystyle \int\limits _{0}^{1}\arctan\left(\frac{\sin\left(\pi k\right)\left(1-x\right)^{k}}{\cos\left(\pi k\right)\left(1-x\right)^{k}-x^{k-1}}\right)\,dx} \end{equation}

Putting everything into a single expression, the inverse for the function $t^{k}+t-1=0$ for t is

\begin{equation} t=1-\left[k+1-\frac{1}{\pi}{\displaystyle \int\limits _{0}^{1}\arctan\left(\frac{\sin\left(\pi k\right)\left(1-x\right)^{k}}{\cos\left(\pi k\right)\left(1-x\right)^{k}-x^{k-1}}\right)\,dx}\right]^{-1} \end{equation}

A graph of this expression with the given approximation is the following

Where you can see that it is a very good approximation, more so for values ​​close to 1

Ref:

-E. E. Burniston, C.E. Siewert. The use of Riemann problems in solving a class of transcendental equations. Mathematical Proceedings of the Cambridge Philosophical Society. 73. 111 - 118. (1973).

-Henrici P., Applied and computational complex analysis, Volume III. Wiley, New York. 183-191 (1986).