Creation/computation of "Two not touch" puzzles

Question

This is a mathematical and algorithmic question, so I hope it is not flagged for failing to be a pure mathematical question.

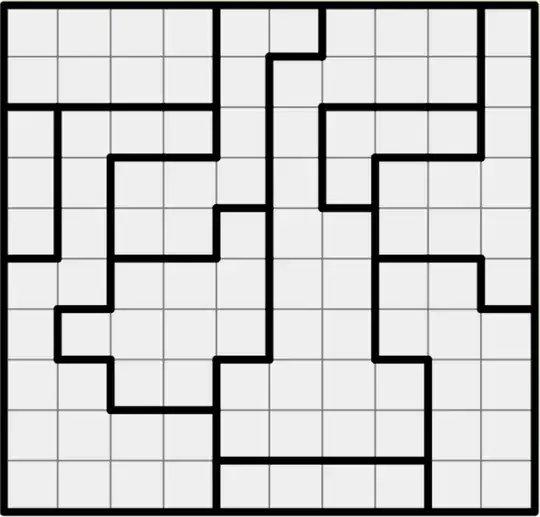
The puzzle "Two not touch" (or Star Battle) consists of a $10 \times 10$ grid array fully tiled with irregularly shaped contiguous regions, for instance:

The task is to place (20) stars in the grid cells such that:

• There are exactly two stars in each row
• There are exactly two stars in each column
• There are exactly two stars in each contiguous tiled region
• No two stars "touch," that is, are adjacent vertically, horizontally, or on diagonally adjacent squares

My question isn't about how to solve such a puzzle. It is instead how to algorithmically/mathematically create a valid puzzle that has a (single) unique solution, as such puzzles ensure.

I have little doubt that the first step is to randomly assign two cells (for "virtual stars"... where the solution stars must fall) in each row and each column in a blank (un-tiled) grid, obeying the "not touch" constraint. This is quite a simple algorithm.

Next comes drawing the tiled regions. It is fairly straightforward to draw contiguous regions that bound just two of the virtual stars.

Question: How does one ensure that the tiled regions admit just a single unique puzzle solution?

Answer 1

I wrote the constructor that made the puzzles in OP's post. Here's how it works in general.

Assume the existence of an algorithm layout() that can generate a randomized Star Battle style grid that divides the 10x10 square into 10 regions. The resulting layout may, or may not be a valid puzzle. Note that this algorithm does not know anything about where the stars should go. There are several ways this algorithm can work.

Also, assume the existence of an algorithm solve() that uses production rules to solve Star Battle puzzles. The production rules are the same kind of pattern-based rules a human might use to to solve the puzzles, such as "if there is a star, the squares around it can be eliminated", "if a container contains two stars, the remaining squares in the container can be eliminated", "if a container has only enough open squares remaining to make two stars, those squares must be stars", etc. I have something like 15 rules for this particular puzzle. They were determined by solving these puzzles manually and observing what patterns I followed. The solve() algorithm is essentially a repeated loop:

1. for each rule, check if the pattern is matched. if so, clear or set one or more squares as dictated by the rule and start the loop over.
2. If, after following a rule, the puzzle is now fully solved, we are done.
3. If the puzzle is still unsolved, and all the rules are examined with no hits, the puzzle is unsolvable or has multiple solutions.

This algorithm can only find a solution when the puzzle has a single unique solution.

I prefer to use Production-rule solvers, because they are better for estimating difficulty, but a general purpose stack-based brute-force solver can also work.

The basic method for construction is what I call a "puzzle sieve" and works like so:

1. Call layout() and produce a candidate layout.
2. Attempt to solve it, using solve()
3. Is it solved? Good you have a valid puzzle and now you know where the stars go.
4. Is it not solved? Go back to step 1.

I could have started with randomized star positions, as OP indicates, but it turns out that the layout algorithm is much simpler if you don't have to work around fixed stars. In either case, the solve() algorithm is necessary to determine solvability and uniqueness, and it will determine where the stars go, so there are no real time savings to placing stars first.

For this puzzle, roughly 98% of the candidates produced will not be valid puzzles. That's okay, the algorithm is fast enough for this particular puzzle.

Answer 2

Here is an outline of an algorithm which would generate such grids, although I make no claims as to how efficient it might be.

1. Start with an empty $n \times n$ grid.

2. "Seed" the grid by assigning some of the cells a value between 1 and $n$.

3. Determine whether the grid allows a solution to an "Expansionist Star Battle", which is Star Battle but you also have to determine the regions as you solve it (where rather than depicting the regions using walls, all cells with the same value are part of the same region).

4. From step 3, identify any backbone components of the solution.

5. If the backbone is the entire grid (both regions and stars), then you have a unique solution and you can erase the stars and the remaining grid is the puzzle.

6. Add the backbone components to the grid. Also fix some of the region assignments in the found solution.

7. Take this new grid and go back to step 3.

8. If at any point you have no solutions, or if you have assigned every cell to a region and you don't have a unique solution, then erase some of the cells and go back to step 3.

This algorithm relies on having a reasonably efficient method for (a) solving "Expansionist Star Battle" (though not necessarily proving its uniqueness) and (b) identifying any fixed parts of its solution, both of which are probably computationally quite hard. I suspect that you can have a setup that starts by doing everything quite approximately and heuristically (e.g. it applies some strict deduction to find the forced parts of the solution, some kind of greedy approach to prove that a solution exists at all, and assigns cells to regions based on some randomised closeness criteria), then when it starts hitting a point where it's not making progress switches to a more sophisticated constraint programming method.