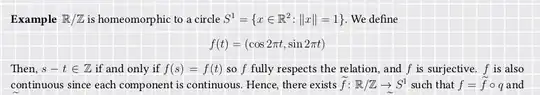0

Reading notes on a course on general topology I have the following enter image description here

which reads that $\mathbb{R} / \mathbb{Z}$ is homeomorphic to $S^1$, where $S^1$ is the unit circle.

Question: Homeomorphisms are between topological spaces. I know what sets they are using but I am not sure about the topologies. Is the text saying that $(\mathbb{R}/\mathbb{Z},\tau_\text{quotient})$ is homeomorphic to $(S^1,\mathcal{P}(S^1))$?

If someone can help me find out what topologies are associated with the sets I would greatly appreciate it.

Martin Sleziak
  • 56,060
Maths Wizzard
  • 2,418

2 Answers2

1

Yes.

If we have a space $X$ and an equivelence relation $\sim$ on $X$, then the standard approach is to endow the set $X/\sim$ of equivalence classes with respect to $\sim$ with the quotient topology induced by the canonical map $q : X \to X/\sim$ given by $q(x) =[x]$ = equivalence class of $x$.

Therefore, whenever such a set $X/\sim$ occurs in topology, you can be sure that it is automatically regarded as a topological space with the quotient topology.

In your example only the quotient topology can assure the continuity of the map $\tilde f : \mathbb R/\mathbb Z \to S^1$ which is induced by $f$.

Let me mention that the notation $\mathbb R/\mathbb Z$ is somewhat ambiguous. In topology, if we are given a space $X$ and a subset $A \subset X$, then $X/A$ usually denotes the set obtained by collapsing $A$ to a point. Formally we have $X/A = X/\sim$ with $x \sim y$ iff $x = y$ or $x,y \in A$. But this is not the interpretation of $\mathbb R/\mathbb Z$. Here it is regarded as the quotient group of the additive group $(\mathbb R, +)$ by its subgroup $\mathbb Z$.

See also $\mathbb{R} / \mathbb{Z}$ is homeomorphic to $S^{1}$ .

Paul Frost
  • 87,968
0

It is standard to regard $S^1$ with the subspace topology of $\mathbb{R}^2$. On the other hand, $$x\sim y \iff x-y\in \mathbb{Z}\iff f(x)=f(y)$$ defines an equivalence relation $\sim$ on $\mathbb{R}$. The quotient topology $\tau_{\text{quotient}}$ on the set of equivalence classes $\mathbb{R}/\mathbb{Z}\stackrel{def}{=}\mathbb{R}/\sim$ is given by either one of the following and equivalent definitions

  1. $U\subseteq\mathbb{R}/\mathbb{Z}$ is open $\iff$ $\pi^{-1}(U)\subseteq\mathbb{R}$ is open.

  2. $\tau_{\text{quotient}}$ is the finest topology such that $\pi$ is continuous.

Where $\pi:\mathbb{R} \to \mathbb{R} /\mathbb{Z} $ is the quotient projection that assings to each $x\in \mathbb{R} $ its equivalence class $[x]$.

R. Pullbacki
  • 716