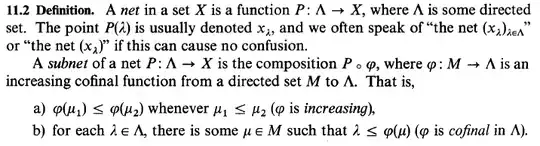Prove that if $X$ is sequentially compact then given any $\epsilon>0$ there exists a finite covering of $X$ by open $\epsilon$-balls.

Question

At the chapter 4-th in the text General Topology Stephen Willard give the following definition

Now the function $\varphi$ in the previoius definition must not be necessary strictly increasing so that with respect this definition a subsequence $(x_{n_l})_{l\in\omega}$ of a injective sequence $(x_n)_{n\in\omega}$ could be costant, that is it is possibile there exists $n\in\omega$ such that $$ n_l=n $$ for any $l\in\omega$. However at the chapter 3-th in the text Topology James Munkres gives the following definition.

which requires that a subsequence of an injective sequence must be injective: anyway sometimes Munkres use the symbol $\subset$ to mean $\subseteq$ so that I supposed that here he does a similar thing but obviously I canno be sure.

Now let's prove that if $X$ is sequentially compact then given any $\epsilon>0$ there exists a finite covering of $X$ by open $\epsilon$-balls.

So I would like to discuss why $(x_n)_{n\in\omega}$ cannot have any convergent subsequence: indeed if $(x_{n_l})_{l\in\omega}$ was a subsequence converging to $x$ then there would exists $l_\epsilon\in\omega$ such that $$ x_{n_l}\in B\Big(x,\frac\epsilon 2\Big) $$ for any $l\ge l_\epsilon$ so that in particular for any $l\ge l_\epsilon$ the inequality $$ \begin{equation}\tag{1}\label{eq:simple1}{d(x_{n_l},x_{n_{l_\epsilon}})\le d(x_{n_l},x)+d(x,x_{n_{l_\epsilon}})<\frac\epsilon 2+\frac\epsilon 2=\epsilon}\end{equation} $$ holds but $(n_l)_{l\in\omega}$ must be strictly increasing by Munkres definition so that we conclude that $(x_{n_l})_{l\in\omega}$ does not converges. So is true that Munkres definition requires that $(n_l)_{l\in\omega}$ is strectly increasing? Is Munkres definittion usual? is Willard definition unusual? If Munkres definition does not requires injectivity how prove that $(x_{n_l})_{l\in\omega}$ does not converges? So could someone help me, please?

Answer 1

We can identify sequences $(x_n)$ in $X$ with functions $x : \mathbb N \to X$, the identification given via $x(n) = x_n$. Thus sequences are also nets in the sense of Willard.

A subsequence of $x = (x_n)$ is then nothing else than a sequence of the form $x \circ \iota : \mathbb N \to X$ where $\iota : \mathbb N \to \mathbb N$ is strictly increasing (and in particular injective). Writing $\iota(k) = n_k$, we have $n_1 < n_2 < n_3 < \ldots$ and $(x \circ \iota)_k = (x \circ \iota)(k) = x(n_k) = x_{n_k}$.

This definition is in fact the standard one.

Nets generalize sequences, but the definition of a subnet differs form that of a subsequence in two aspects:

1. A subnet is allowed to have a different index set than the original net.

2. The "index function" $\varphi : M \to \Lambda$ is required to be increasing (not strictly increasing) and cofinal.

Willard's definition of a subnet is indeed the standard one. But let us emphasize:

• A subnet of a sequence $(x_n)$ may no longer be a sequence.

• Even if we consider only $\mathbb N$-indexed subnets of $(x_n)$, there are index functions which are not strictly increasing. This means that $\mathbb N$-indexed subnets are again sequences, but not necessarily subsequences of $(x_n)$. But of course each strictly increasing $\iota : \mathbb N \to \mathbb N$ is increasing and cofinal, thus the set of subsequences of $(x_n)$ is a proper subset of the set of $\mathbb N$-indexed subnets of $(x_n)$.

The sequence $(x_n)$ constructed by Munkres has the property $d(x_j,x_i) \ge \epsilon$ for all $j, i$ such that $j > i$. Thus no subsequence $x \circ \iota$ of $x = (x_n)$ can be a Cauchy sequence (simply because $\iota(j) > \iota(i)$ for $j > i$) and thus no subsequence converges. His statement that $(x_n)$ cannot have a convergent subsequence because no ball of radius $\epsilon/2$ contains at most one $x_n$ is correct (as you proved in your question), but it is actually unnecessary to mention it.

In your answer you correctly show that $(x_n)$ cannot even have a convergent $\mathbb N$-indexed subnet. This is in fact a more general result than that for the subsequence case.

Actually we can prove the following theorem valid for all sequences $(x_n)$ in an arbitrary topological space $X$:

• If $x = (x_n)$ has a convergent subsequence if and only if it has a convergent $\mathbb N$-indexed subnet.

The "only if" part is trivial. For the "if" part let $x \circ \varphi$ be convergent $\mathbb N$-indexed subnet (with limit $\xi$). Here $\varphi : \mathbb N \to \mathbb N$ is an increasing and cofinal function. By cofinality the image $A = \varphi(\mathbb N)$ is an infinite subset of $\mathbb N$, thus there is a strictly increasing $\iota : \mathbb N \to \mathbb N$ such that $\iota(\mathbb N) = A$. We claim that the subsequence $x \circ \iota$ converges to $\xi$.

Since $x \circ \varphi$ converges to $\xi$, each open neighborhood $U$ of $\xi$ in $X$ admits $N$ such that $(x \circ \varphi)(n) \in U$ for $n > N$. Choose $K$ such that $\iota(K) = \varphi(N)$. For each $k > K$ we have $\iota(k) = \varphi(n)$ for some $n$. But $\varphi(n) = \iota(k) > \iota(K) = \varphi(N)$ which implies that $n > N$ since $\varphi$ is increasing. This shows that $(x \circ \iota)(k) = (x \circ \varphi)(n) \in U$ for $k >K$.

Answer 2

First of all we observe that if $\iota$ is cofinal map of $\omega$ to $\omega$ then for any $n\in\omega$ there exists $m(n)$ such that $$ \iota(n)<\iota(n)+1\le\iota\big(m(n)\big) $$ so that now there exists $l\in\omega$ such that $$ n_{l_\epsilon}< n_l $$ and in particular by increase we can suppose that $l>l_\epsilon$ but in this case it would be $$ d(x_{n_l},x_{n_{l_\epsilon}})\ge\epsilon $$ which surely inconsistent with $(1)$.