I am not into mathematics so a request to answer in simpler terms. I am using radial basis function (RBF) for interpolating some data points using multiquadratic basis function. Considering $n$ data points, my RBF model looks like: $RBF(x)=\sum\lambda_i\phi(x,x_i)$, where $\phi$ denotes the multiquadratic (MQ) basis function as follows: $\phi(x,x_i)=\sqrt(r^2 + C^2)$, where $r$ is the euclidean distance between point of inference ($x$) and center point $x_i$. I understand that $C$ influences the shape of the RBF surface. I observe that when $C=0$, the response surface changes curvature around the center points sharply, but as I increase $C$ to say $0.05, 0.1, 0.2, ...$, the smoothness of the surface increases and the curvature of the surface does not change instantly around the center point. How can I justify such a behavior of the response profile for increasing values of $C$ in a multiquadratic radial basis function model.
For clarity, I have attached 2 figures (one when $C=0$ and other when $C=0.1$) as an example.
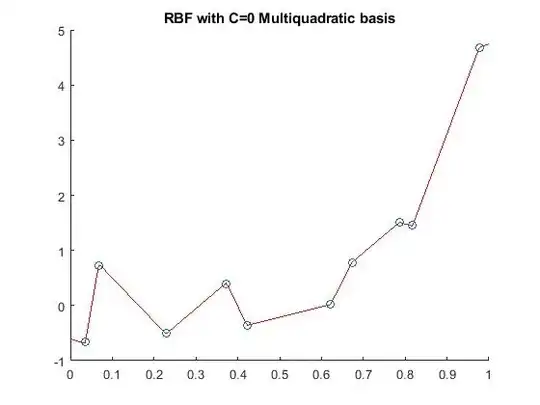 $C=0$" />
$C=0$" />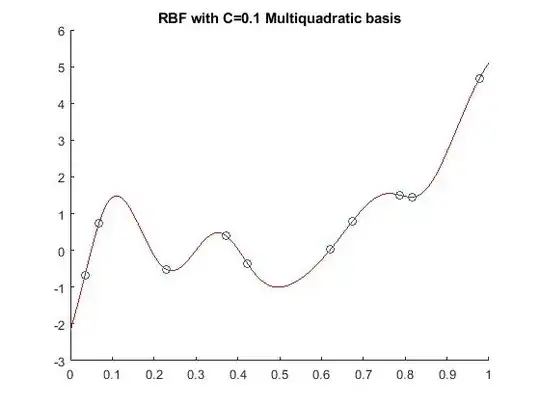 $C=0.1$" />
$C=0.1$" />