ZigZag Function's formula?

Question

I'm searching the formula/expression of the "zigzag" function that returns the following curve/graph:

$\quad\qquad\qquad\qquad\qquad$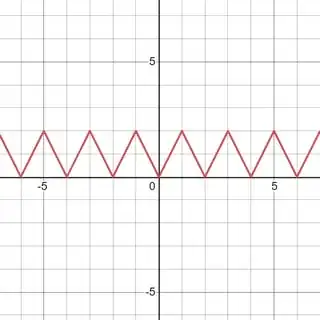

I'm looking for

1. that's trigonometric and
2. that's non-trigonometric

Please help. Hopefully one or both are simple enough (not too complex).

---

Why I'm looking for the above function/graph?
In this post it struck me to at least confirm which result was correct by drawing the above graph for both the objects and then counting all the point of intersections. Thus, confirming the correct answer. But while going to GeoGebra I realized my ignorance/ineptitude to draw such a graph. Though I think I used to be able to draw/know one.

Answer 1

$$f(x)=\begin{cases}x-\lfloor x\rfloor&\lfloor x\rfloor\equiv_20\\1+\lfloor x\rfloor-x&\lfloor x\rfloor\equiv_21\end{cases}$$

This is the periodic extension of $x\mapsto|x|$.

A non-piecewise definition would be:

$$f(x)=\frac{1-(-1)^{\lfloor x\rfloor}}{2}+(-1)^{\lfloor x\rfloor}(x-\lfloor x\rfloor)$$

To get a trigonometric sharp zig-zag as drawn you’d need to use a Fourier series or some similar idea. No simple trigonometric function will produce the zigzag shown there.

Answer 2

It is more commonly known as “triangle wave”:

https://en.m.wikipedia.org/wiki/Triangle_wave

(Not to be confused with the “sawtooth wave”.)

Answer 3

(1) $$x \mapsto \frac2\pi \arccos \cos \pi x$$

(2) $$x \mapsto 4 \left\vert \frac{x}2 - \left\lfloor \frac{x - 1}2 \right\rfloor \right\vert$$