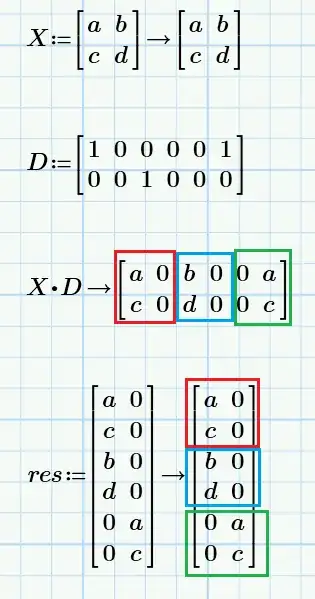0

There are 2 matrices and the result of their product:

$X=\begin{bmatrix}a & b \\ c & d\end{bmatrix}$

$D=\begin{bmatrix}1 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 & 0 & 0\end{bmatrix}$

$X \cdot D=\begin{bmatrix}a & 0 & b & 0 & 0 & a\\ c & 0 & d & 0 & 0 & c\end{bmatrix}$

The desired result looks like this:

enter image description here

My question: are there alternative, simpler operators that do the desired transformation?

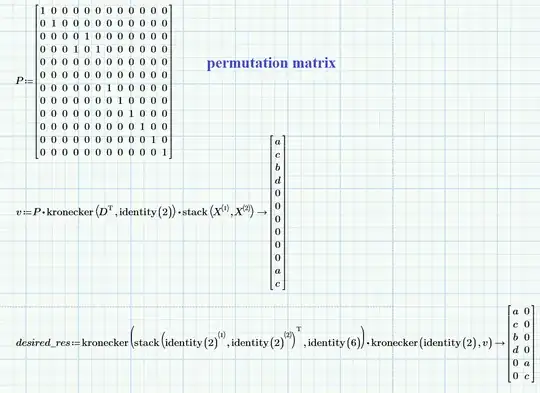
My attempt: I first vectorized the original result, then "cut and stitched" in a new way [https://math.stackexchange.com/a/3122442/656085]:

enter image description here

https://dropmefiles.com/avpwH - here is the file from Mathcad Prime 8

ayr
  • 793

1 Answers1

1

Partition $D$ into 8 column vectors, so $XD$ is just$[Xv_1, ... , Xv_8]$ $$X \begin{bmatrix}e\\f\end{bmatrix}$$ is the column vector $e$ column 1 of $X$+$f$ column 2 of $X.$

P. Lawrence
  • 5,768
  • I didn't quite understand your answer. Could you describe it in a little more detail: what is $e$ and $f$, what is the function $X + f$, etc. – ayr Oct 04 '22 at 11:53
  • 1
    ($e$ co[umn 1 of $X$) + ($f$ column 2 of $X$). Write $v_1$ as $$\begin{bmatrix} e\f \end{bmatrix}$$.Similarly for $v_2, ... ,v_8$. – P. Lawrence Oct 04 '22 at 13:41
  • Thank you! That's cool – ayr Dec 21 '22 at 13:43