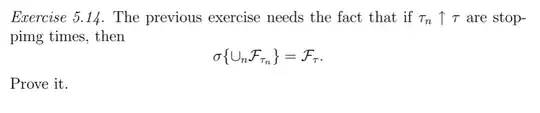I was reading in Varadhan's book: probability theory and where I found the following exercise $5.14$. I also came across a similar question: How to prove $\mathcal F_T \subseteq \sigma(\bigcup_n \mathcal F_{T_n})$?
Can we claim that $\Omega\subset\bigcup_{n \in \mathbb{N}}\{\tau_n=\tau\}$? Why ? In case the claim was wrong how can we prove that $\mathcal{F}_{\tau} \subset\left(\bigcup_{n \in \mathbb{N}}\mathcal{F}_{\tau_n}\right)$?