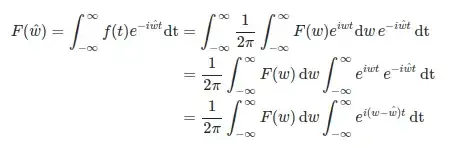0

Why the second line can be done, please? Why is the exponential function of w in the integral $\mathrm{dt}$ only (not in $\mathrm{dw}$)?

enter image description here

Edit after the answer:

I am asking about the procedure in the second answer here. The last step should be

$$ \int_{-\infty}^{\infty} F(w) \delta (w-\hat w) {\rm d}w = \frac{1}{2\pi}\int_{-\infty}^\infty F(w) \left(\int_{-\infty}^\infty e^{i(w-\hat{w})t}\,\rm {d}t \right) \,{\rm {d}w}$$

After derivation of the equation, it is:

$$\frac{1}{2\pi}\int_{-\infty}^\infty e^{i(w-\hat{w})t}\,\rm {d}t= \delta (w- \hat w) $$

Is that correct?

What if there were sums instead of integrals, please? How to get

$$\frac{1}{2\pi}\sum_{t} e^{i(w-\hat{w})t}= \delta (w- \hat w) $$ ?

Elena Greg
  • 115
  • Because the decision is made to integrate first over $t$, so we must collect all terms depending on it. At this moment $F(w)$ is just a constant, so we put in the integral over $w$. – M. Wind Sep 27 '22 at 18:26
  • It just seems like a bad way of writing it. The resultant would be inside the $w$ integral. – Crypton Sep 27 '22 at 18:26
  • I think your edit should be a separate new question. – Anne Bauval Sep 27 '22 at 19:05

1 Answers1

2

It is an incorrect (but alas frequent) notation. The correct one is: $$\begin{align}F(\hat w)=\int_{-\infty}^\infty f(t)e^{-i\hat wt}\mathrm dt&=\int_{-\infty}^\infty\frac1{2\pi}\left(\int_{-\infty}^\infty F(w)e^{iwt}\mathrm dw\right)e^{-i\hat wt}\mathrm dt\\&=\frac1{2\pi}\int_{-\infty}^\infty F(w)\left(\int_{-\infty}^\infty e^{iwt}e^{-i\hat wt}\mathrm dt\right)\mathrm dw\\&=\frac1{2\pi}\int_{-\infty}^\infty F(w)\left(\int_{-\infty}^\infty e^{i(w-\hat w)t}\mathrm dt\right)\mathrm dw.\end{align}$$

Anne Bauval
  • 49,005