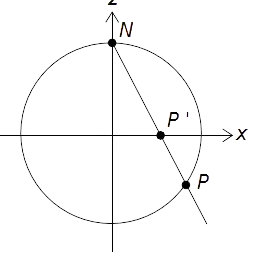
It seems to be a dumb question (according to my research), but I do not see (in algebric way) why stereographic projections preserve angles.
There is a really good paper here that gives a geometric perspective, but is not exactly what I am looking for.
Could someone give me a hand on this algebraic proof?
$f(x,y) = \frac{1}{g}(2x,2y,x^2+y^2-1) $ where $g=x^2+y^2+1$.
Hence we have a claim that $$\langle Df\ e_1,Df\ e_2\rangle =0 \ {\rm and}\ |Df\ e_1|=|Df\ e_2|=\frac{2}{g},$$ where $e_i$ is a canonical basis, which implies that $f$ is conformal.
Proof : \begin{align*} Df e_1=\frac{\partial f}{\partial x}&=\frac{1}{g}(2,0,2x) + (2x,2y,x^2+y^2-1) (-2x)g^{-2} \\&=\frac{2}{g^2} (-x^2+y^2+1,-2xy,2x ) \end{align*}
By symmetry we have $$ Df e_2 = \frac{2}{g^2} (-2xy,x^2-y^2+1,2y) $$
Remaining is simple computation so that we have the proof.
Silly me didn't read the question before answering, and provided the geometric answer, not the algebraic. I can't seem to delete it, so I'll just have to let it stand.
I you look at a projection, the distortion of angles depends on the angle the plane or tangent plane makes with the direction from which you are viewing it (or ray of projection): the more tilted the plane is, the more compressed it will look along the direction it is tilted from your point of view.
For the sphere (or circle as in the figure), these angles are the angle the line $NP$ makes with the $x$-axis at $P'$, and with the circle at $P$.
The circle has the property that the angle a $P'$ and the angle at $P$ are the same (when measured at opposite sides): both are the same as the angle the line $NP$ makes with the circle at $N$.
