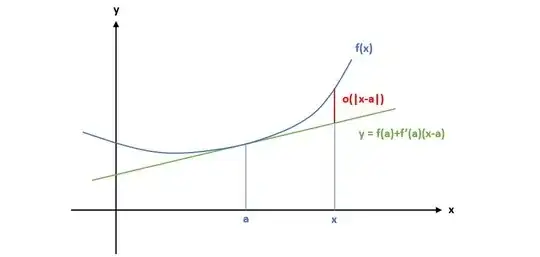
I am a graduate student and currently studying functions of several variables.I am mainly following Paliogiannis and Moskowitz.When they are introducing differentiability for function of several variables,they are drawing similarity with one variable differentiability.We say that $f:\Omega\subset \mathbb R\to \mathbb R$ $(\Omega$ open$)$ is differentiable at $a\in \Omega$ if the limit $\lim\limits_{x\to a}\frac{f(x)-f(a)}{x-a}=f'(a)$ exists (finitely).The same statement can be equivalently written as, $\lim\limits_{x\to a}\frac{|f(x)-f(a)-f'(a)(x-a)|}{|x-a|}=0$ which is equivalent to saying that $f(x)=f(a)+f'(a)(x-a)+o(|x-a|)$.Then they say that $f(x)\approx f(a)+f'(a)(x-a)$ is a good approximation of $f(x)$ near $a$.They say that the numerator $|f(x)-f(a)-f'(a)(x-a)|\to 0$ faster than the denominator $|x-a|\to 0$.I want to understand what is the significance of 'good approximation'?The error term goes to $0$ faster than $x\to a$,why is this being called 'good'?Can someone give me a little motivation?
Asked
Active
Viewed 160 times
1
-
I think the answer given by Paramanand Singh here https://math.stackexchange.com/questions/2577281/good-linear-approximation-criteria?rq=1 gives some insight. – Kishalay Sarkar Sep 04 '22 at 06:21
-
1There is no rigorous definition of "good" and what "good" is depends on the purpose of the approximation and which accuracy is needed. – Peter Sep 04 '22 at 12:44
1 Answers
0
When derivative exists, we can say that $f(x)\approx f(a)+f'(a)(x-a)$ in the sense that we can consider the following linear approximation
$$y(x)= f(a)+f'(a)(x-a)$$
which is the tangent line for $f(x)$ at the point $x=a$.
This approximation is good in the sense that the difference
$$f(x)-y(x)=o(|x-a|)$$
as $x \to a$, goes to zero more rapidly than the linear quantity $|x-a|$ (or it is equal to zero when $f$ is linear).
By Taylor's series the concept can be generalized to obtain higher order polynomial approximation for $f(x)$ at a given point $x=a$.
For functions of two variables the linear approximation becomes a plane and also Taylor's series can be extended to several variables.
Refer also to the related
user
- 162,563