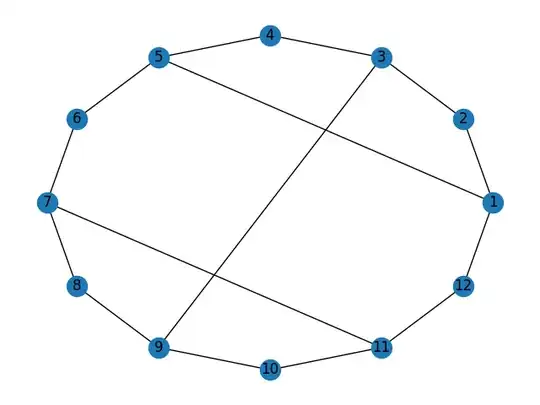
I'm not fully understanding the concept of retracts, I think. For example, does this graph have any possible retracts? It seems like it doesn't to me, but I'm not sure how to check.
Also, what if instead of each of $2, 4, 6, 8, 10,$ and $12,$ there were paths of arbitrarily long length between $1$ and $3, 3$ and $5, 5$ and $7, 7$ and $9, 9$ and $11,$ and $11$ and $1$? Would there be retracts then?