Number of solutions of $|\log_e{|x-2|}|+x^2-2x-35=0$

Question

Find the number of solutions of the given equation: $$|\log_e{|x-2|}|+x^2-2x-35=0$$

While studying the topic "Graph Transformation", this question cam up and the answer was said as 4.

Out of curiosity, I went to Geogebra, and there I saw the answer should be 2 instead!
Here's my simple attempt in GeoGebra for confirmation.

1. Isn't there a way that complements the graph so as to confirm the answer?
   
2. How can this question be solved without the use of graphs?

Please help.

Answer 1

Okay, so the trick to dealing with the question is to begin by figuring out where the solution can exist rather than where exactly the solution is.

We can rearrange the equation as:

$$ | \log_e |x-2| | = -(x^2 - 2x -35)$$

The reason I did this was that I have an absolute value, rearranging like this tells me I have to focus only on the part where RHS is positive. So, we have to solve the inequality:

$$ -(x^2 - 2x - 35) \geq 0 \iff x^2 - 2x -35 \leq 0$$

Now, I'll tell you are pretty uncommon trick: Consider the quadratic $q(x)= x^2 - 2x -35$, if we consider $\lim_{x \to \infty} q(x)$ then we it should be that the $x^2$ term dominates the value. Since the $x^2$ term has positive coefficient, $ \lim_{ x \to \infty} q(x)$ is some positive value. This means that the whole quadratic is negative in the region between the roots (it's in some finite place of $\mathbb{R}$). I find the solution as:

$$ - 5 \leq x \leq 7 \tag{1}$$

Before removing the absolute value on LHS, we have to see when the function is positive and when it's negative. We have :

$$- \log_e |x-2| \leq 0 \iff |x-2| \leq 1 \iff 1 \leq x \leq 3 \tag{2}$$

And,

$$ \log_e |x-2| > 0 \iff |x-2|>1 \tag{3}$$

---

Now, since domain must work for both sides, we have to intersect (1) with (2) and intersect (1) with (3), and simplfy.

1. On the interval $[1,2)\cup(2,3]$, we have:

$$- \log_e (|x-2|) = - (x+5)(x-7)$$

2. On the interval $ \left(-5,1 \right] \cup \left[3,7\right)$ , we have:

$$ \log_e (|x-2|) = -(x^2 -2x -35) $$

Now, we can split into further sub cases by expanding out the piece input and then use increasing/ decreasing arguments on the simplfied subsets to solve. Or, one can directly go for a graphical solution after (1):

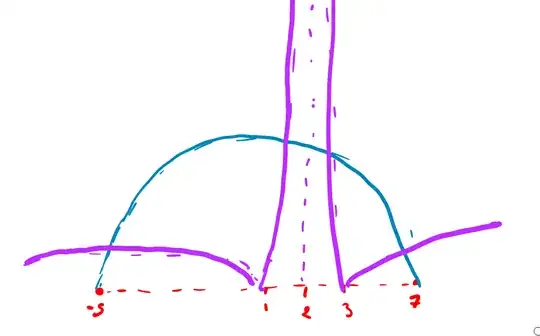
(1) told me how the parabola looks like, and then it's just drawing grap hof $\log_e$ using experience.