How does the path connectedness in a topology book relate to the path connectedness described in a typical vector calculus book?

Question

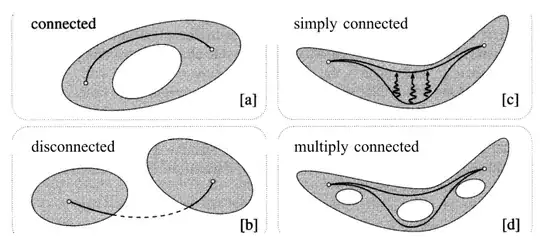
A set $S$ is said to be connected (see [30a]) if any two points in S can be connected by an unbroken curve lying entirely within $S$. Conversely, if there exist pairs of points that cannot be connected in this way (see [30b]), then the set is disconnected. Amongst connected sets we may single out the simply connected sets (see [30c]) as those that do not have holes in them. More precisely, if we picture the path connecting two points in the set as an elastic string, then this string may be continuously deformed into any other path connecting the points, without any part of the string ever leaving the set. Conversely, if the set does have holes in it then it is multiply connected (see [30d]) and there exist two paths connecting two points such that one path cannot be deformed into the other.

Page-92, 93 , Neeedham Visual complex Analysis

My doubt about this section came when I started reading about Topology from Munkres. The above text seems to be about topological space being path connected but my question is, how does one describe holes (and classification of space based on that) as shown above using the topological path connectedness idea?

Path connectedness (deftn):The space $X$ is said to be path-connected if there is exactly one path-component, i.e. if there is a path joining any two points in $X$ source

Answer 1

As mentioned in the comments, connectedness or path-connectedness are not really the key in the description of holes, which —at least in the case of the plane— reduces to the study of simply-connectedness.

And your book is right: in Topology, a space is said to be simply-connected iff it is connected and for any two continuous paths in the space with the same endpoints, one can be continuously deformed into the other while not leaving the space, leaving the endpoints fixed during the process. Of course, this definition needs to be a little more rigorous, but you get the idea.

Finally, since I assume you are interested in the study of subsets of $\mathbb{C}$, here are some equivalent definitions of simply-connectedness for open subsets of the plane, and I’m sure you are going to come across some of them in the future:

Proposition. Let $\Omega\subsetneq\mathbb C$ be open and connected. The following are equivalent:

1. $\Omega$ is simply connected.
2. Any closed continuous path in $\Omega$ can be continuously shrunk to a point.
3. The complement of $\Omega$ in $\mathbb {C}_\infty = \mathbb{C}\cup\{\infty\}$, the Riemann sphere, is connected.
4. For any piecewise $C^1$ closed path $\gamma$ in $\Omega$, and for any $a\notin\Omega$, $\operatorname{Ind}(a;\gamma)$ (the winding number of $\gamma$ around $a$) is equal to zero.
5. $\Omega$ is homeomorphic to the unit disk $D=\{z\in\mathbb{C} : \lvert z\rvert<1\}$.
6. $\Omega$ is conformally equivalent to the unit disk $D$, i.e., there exists a holomorphic bijection between $\Omega$ and $D$.

1 and 2 are true for any topological space, which can be seen in any basic algebraic topology text. The equivalence between 3 and 4 is also well-known in basic Complex Analysis. The equivalences between 5, 6 and any of the rest are just different versions of the Riemann Mapping Theorem. Maybe 1$\iff$3 is the most unusual one. Here is a reference.

Answer 2

Needham explicitly writes that he "introduces some terminology which we need for describing sets of points in $\mathbb C$". So $S \subset \mathbb C$.

Anyway, you are right, what he defines is path connectedness. But even this is a bit vague; what is the precise meaning of an "unbroken curve lying entirely within $S$"?

As Jyrki Lahtonen comments, the standard definition of connectness in topology is the non-separability of a space into two disjoint non-empty open subsets. See Munkres §23. Path connectedness implies connectedness, but the converse is not true. See Munkres Example 2 on p. 160 which deals with a certain subset of $\mathbb C$.

So is Needham's definition of connectedness a wrong one? Of course every author is free to use his own terminology, but in my opinion he should adhere to commonly accepted standards. Needham does not do this, and for arbitrary subsets $S \subset \mathbb C$ we get a non-standard interpretation of connectedness. However, in complex analysis on usuall works with open subsets of $\mathbb C$ and for these connectedness and path connectedness agree. The reason is that open subsets of $\mathbb C$ are locally path connected. See Munkres Theorem 25.5. But let me emphasize that Needham's definition is nevertheless, to put it mildly, exotic even if it produces the same result for open subsets of $\mathbb C$.

The concept of a hole is also a very vague one, and for general topological spaces one has to use the machinery of algebraic topology to give an interpretation. But it is hard to say whether the intuition of a hole is exactly that what is measurable via algebraic topology.

What Needham tries to define is the fundamental group of a space. See Munkres Chapter 9 for a precise definition. Also have a look at Characterizing simply connected spaces. A space which is not simply connected may be called multiply connected, but this wording seems to be limited to complex domains. See here. At least I have never seen it in textbooks on (algebraic) topology.

Answer 3

You need the concept of homotopy to define simply connected subsets. This is the formalization of the idea of "continuously deforming the string" that Needham mentions. It has everything to do with paths and you'll likely find it in your topology textbook.