6

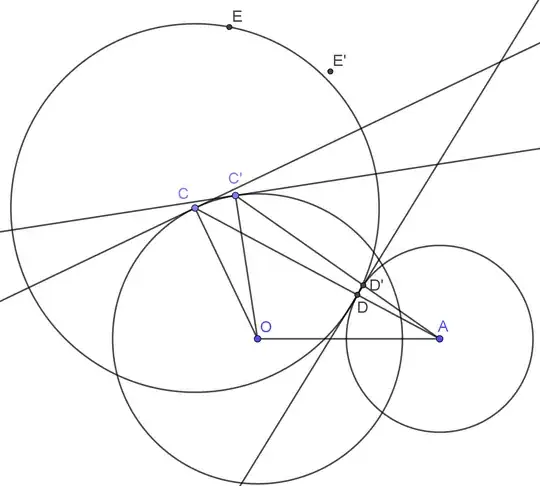
$O,A$ and $B$ are arbitrary points on the plane. Point $C$ moves on the circle with center $O$ and radius $OB$.

Construct a circle with center $C$ and externally tangent to the circle with center $A$ and radius $AB$. Let the tangency point be $D$.

$E$ is the point on the circle $C$, such that $OC∥DE$.

$Γ$ is the locus of the point $E$ [as $C$ moves on the circle $O$].

Prove that $Γ$ is always tangent to the circle $C$ [as $C$ moves on the circle $O$].

tangent

I found this when trying to geometrically construct a point on $Γ$ which is the envelope of circle $C$.

The equation of $Γ$ when $B(1,0),A(2,0)$

$20 x^8 y^2-16 x^7 y^2+40 x^6 y^4-444 x^6 y^2-24 x^5 y^4+708 x^5 y^2+40 x^4 y^6-666 x^4 y^4+1706 x^4 y^2 -16 x^3 y^6+708 x^3 y^4-3752 x^3 y^2+20 x^2 y^8-444 x^2 y^6+1834 x^2 y^4+834 x^2 y^2+4 x^{10}-4 x^9-111 x^8 +236 x^7+526 x^6-1876 x^5+1537 x^4+572 x^3-1716 x^2-4 x y^8+236 x y^6 -1876 x y^4+1596 x y^2+1072 x+4 y^{10}-111 y^8+654 y^6-703 y^4-580 y^2-240=0$

Mathematica code:

GroebnerBasis[{(-c + x)^2 + (-s + y)^2 == (-1 + u)^2, 
  s (2 (-1 + v) + x) - c y == 0, c^2 + s^2 == 1, 
  u^2 == (-2 + c)^2 + s^2, (5 - 4 c) v^2 == 1}, {x, y}, {c, s, u, v}]
hbghlyj
  • 5,361
  • Depending upon setup, parametric equations for $E$ aren't terrible. Differentiating to get the tangent vector and determining that it's perpendicular to $EC$ is a little ugly, though. I'm looking for ways to streamline the calculations. – Blue Aug 20 '22 at 02:53
  • 1
    I'm not sure why you would consider this surprising. To me it seems just what one would expect. A small change in $C$ is going to engender small changes in $D$ and therefore in $E$. The circle centered at $C$ passing through $E$ barely changes as well. This small movement of $E$ along $\Gamma$ surely should approximate that circle (away from the two cusps where $\Gamma$ has no tangent). – Paul Sinclair Aug 21 '22 at 14:34

1 Answers1

1

This is an answer expanding @PaulSinclair 's comment.

Make a copy $C',D',E'$ of $C,D,E$.

As $C'\to C$, line $EE'\to$ tangent of $\Gamma$ at $E$, we want to show it is $t_E$, the tangent to circle $C$ at $E$.

Since $D$ and $D'$ are points on circle $A$, when $D'\to D$, the line $DD'\to$ the tangent to circle $A$ at point $D$, which is the same as $t_D$, the tangent to circle $C$ at point $D$.

Point $E$ is the reflection of $D$ across $t_C$, the tangent to circle $O$ at $C$.
Point $E'$ is the reflection of $D'$ across $t_{C'}$, the tangent to circle $O$ at $C'$.
$t_{C'}\to t_C$, so the limit of line $EE'$ is the reflection of the limit of the line $DD'$ across $t_C$,
so the limit of line $EE'$ is the reflection of $t_D$ across $t_C$, so it is $t_E$.

hbghlyj
  • 5,361