Why do we need a Lie derivative of a vector field?

Question

Lie derivative of a smooth vector field $Y$ in the direction of a smooth vector field $X$ is defined (at least in our geometry course) as $L_X Y = \frac{d}{dt}\mid_{t=0} (\psi_\star Y)$ where $({\psi_t}_{t \in I})$ is the local flow of $X$ and $\psi_\star$ is the pushforward of $\psi$, which is defined as the differential $d\psi$.

To my understanding, the definition says that we take the "small change" (derivative) of the local flow corresponding to "small change" in $Y$ (this is my interpretation of the $(\psi_\star Y)$. And that we make one more derivative of this, that is, one "small change", this time corresponding to change in $t$ (this part is the $\frac{d}{dt}$.)

My question is: Do I understand this correctly? Or what is a better intuition behind this?

And also, why do we even need to see how the $L_X Y$ look? What does it tell us to know how one vector field changes and it is somehow connected to changing the other vector field? I don´t understand why this is useful.

Thank you very much!

Answer 1

1. One aspect where the Lie derivative is useful, is in finding isometries of a Riemannian manifold. If the Lie derivative of the metric along a vector field vanishes, then the flow of that vector field is a one parameter family of isometries of the underlying Riemannian manifold, and the vector field is called a killing vector. there's also an analogue of this in symplectic geometry; the Lie derivative of the symplectic form along a Hamiltonian vector field vanishes and has very important geometrical and physical consequences in Hamiltonian mechanics.

2. There are several aspects to the definition of Lie derivative. The obvious one being is that it is a way to differentiate tensor fields that doesn't require any extra structure (unlike the covariant derivative). It only uses the flow defined by vector fields. So in some sense, it is a natural operation that one could do on smooth manifolds (much like exterior differentiation on forms).

3. The Lie derivative has a very clear geometric interpretation: I am going to deliberately ignore manifold subtleties (like the fact that you can't add points) to make it as clear as possible but this can all be justified. So say you have two vector fields $X$, and $Y$ and you want to calculate $L_YX$. Let $\phi^Y_t$ be the flow generated by $Y$ and $\epsilon$ be a very small number. If you draw the vector $\epsilon Y$ emanating from point $p$ and its tip to coincide with the point $q$, then $d\phi^X_t(\epsilon Y)$ is exactly the different vector $\phi^X_t(q)-\phi^X_t(p)$; that is, you can interpret it exactly as deforming the vector in accordance to where it sends the tail and tip of the vector under the flow. If you interpret the flow as a river and the vector as a tiny flexible stick (flexibility is important since the vector can shrink under the flow; hence a tiny rigid stick won't do it); then $d\phi^X_t(\epsilon Y)$ is exactly what you would get if you let it naturally go along the flow (allowing for change in size as well). Then the Lie derivative is exactly the rate of change of that whole process; so it can be summed up as the rate of change of deformation of a tiny vector which is under the influence of the flow.

To convince yourself of all this in detail it is helpful to do the following exercise:

In the plane $\mathbb{R}^2$ take $X=\dfrac{\partial }{\partial x}$ , $Y=-y\dfrac{\partial }{\partial x}+x\dfrac{\partial }{\partial y}$

Compute the flow $\phi^Y_t$ and draw integral curves of $Y$ (they are circles).

Compute $d\phi^Y_t(\epsilon X)$; this would be the "tiny stick" I referred to. Observe its Lie dragging as a function of $t$; notice how the vector (which starts by pointing in the $x$-direction) literally rotates with the flow; this is what Lie dragging is all about. Compute the lie derivative and notice how its just the rate of change of that drag.

Remark: Notice that $X$ is a constant vector field; so it's covariant derivative vanishes, this is because parallel transport doesn't change the vector unlike Lie transport. This is also why Lie derivative is not $C^{\infty}$ linear but the covariant derivative is.

@Deane: This turned out to be too long for a comment so:

Yes I see what you mean; but I don't think it's that much of a problem. Regarding the skew symmetry yes it has quite a concrete visualization. If we work on $\mathbb{R}^n$, and have two vector fields $V$, $U$, scale them down such that they have lengths $\epsilon$, and $\delta$ respectively (this is just to be able to use infinitesimal arguments); then $\dfrac{\partial V}{\partial U}$ (rate of change of $V$ along $U$) is a vector emnating from the tip of $U$, and $\dfrac{\partial U}{\partial V}$ is a vector emnating from the tip of $V$. Now $U$ +$\dfrac{\partial V}{\partial U} \ne V +\dfrac{\partial U}{\partial V}$ (i.e, the paralellogram doesn't close). The commutator/Lie bracket is exactly the thing that closes this. Its antisymmetry reflects the fact that if you do the reverse process then you get minus that vector. Again this can all be checked by simple examples; to that end I invite you to work with the normalized polar vector fields (which is a non-holonomic frame); apply the above arguments and see how all this plays out. In a manifold setting we use flows instead of Euclidean parallel transport. This can also be seen by expanding $\phi^X_{-t} \circ \phi^Y_{-t} \circ \phi^X_{t} \circ \phi^Y_{t}$ (or the pullback version of it) in powers of $t$; you'll notice that the leading term is the Lie bracket; i.e., if you go $t$ along flow of $Y$ then $t$ along $X$ then back $-t$ along $Y$ and then $-t$ along $X$ and you don't return to the same point then the Lie bracket is the leading term which is also the Lie derivative.

Answer 2

Relation of Lie derivative to connection

1. We do not need connection coefficients to write down the Lie derivative. However, if we have a torsion free connection $(\nabla)$ , we can express the Lie derivative as:

$$ L_V \eta = \nabla_{V} \eta - \nabla_{\eta} V$$

2. The Lie bracket can actually be considered as a zero curvature connection with torsion. (in a related sense to the normal connection) for group manifolds

Interpreting the Lie derivative

1. The Lie Bracket interpretation

To understand the Lie derivative, it can be done by understanding an object known as the Lie Bracket of two vector fields:

$$ L_{V} \eta=\left[ V, \eta \right]$$

Now, what is this? The key to understanding it is to think of vector fields as group elements over a manifold as flows pushing the points around by their flows as group actions.

$\hspace{3cm}$

Let's suppose we have a function $f$ which maps points in the chart to numbers, now if we flow the points on the manifold as $I+ \epsilon \eta$ where $I$ is the identity, $\epsilon$ is a tiny number and $\eta$ is a vector on the manifold, the function changes it's value to :

$$ (I+ \epsilon \eta) f= f + \epsilon \eta f$$

Now, suppose we were to consecutively flow the points on the manifold by an infinitesimal vector field $\epsilon \chi$, then our function's value would change by :

$$(I+ \epsilon \chi ) (I+ \epsilon \eta) f = \left (I + \epsilon ( \eta + \chi) + \epsilon^2 \chi \eta \right) f$$

Now the $\epsilon$ order term just shows the parellogram law holds even under these flowy situations.

$\hspace{3cm}$

To really reveal the group structure, we must check the commutator:

$$ \left[ x,y \right]= xy x^{-1} y^{-1}$$

We can find:

$$ (I+\epsilon \chi) (I+ \epsilon \eta) ( I + \epsilon \chi)^{-1} (I+ \epsilon \eta )^{-1}= I+ \epsilon^2 ( \chi \eta - \eta \chi)= I+ \epsilon^2 \left[ \chi , \eta \right]$$

These brackets denote the lack of gap closing by the two vector fields :

$\hspace{2cm}$

2. The dragging interpretation:

$\hspace{3cm}$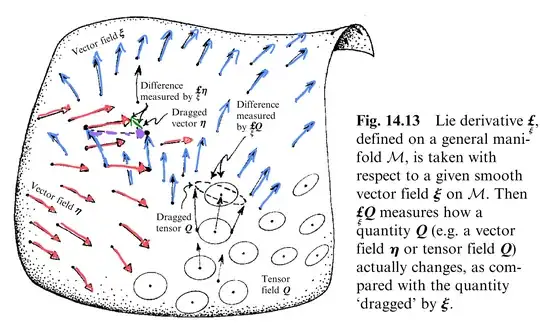

Dragged along is the purple vector, green is the difference.

References: Roger Penrose , Road to Reality, Chapter-13 and 14

3. Short and sweet interpretation for Lie derivative of vector fields

The Lie bracket measures the failure of 'mixed directional derivatives' to commute.

Page-36 of John Baez's Gauge Fields, Knots and Gravity

Utility of the Lie derivative

1. To my knowledge for proving certain vector calculus identities using differential forms, the only way to do it using Lie derivative. See here