0

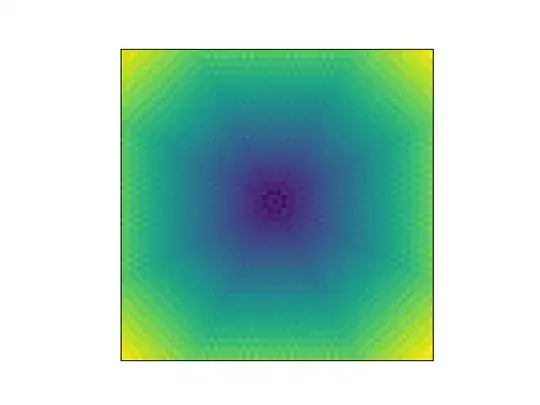
So, I'm looking at a problem that involves finding the minimum number of jumps that a knight would have to make to move from one square to another on the board.

Simplifying the problem to just cases where the knight starts at the origin, I've noticed that for cases of nJumps >= 5, there is a pattern that arises with octagonal shells.

darker colors represent fewer jumps

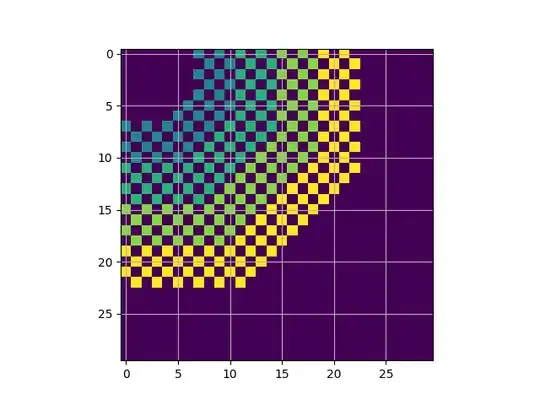
This pattern is even more clear when I just look at specific shells. For instance, below are the squares that can be reached in a minimum of 5 jumps.

Just squares for which the minimum number of jumps is 5

I'm trying to figure out an equation that can be used to convert from the square coordinates to the number of jumps, but I can't seem to figure out a good equation for the shells.

I tried to use bounding boxes, but that didn't seem to work for the diagonal parts of the shells (I know it's probably possible but I just couldn't figure it out).

Then I noticed that I could use diagonals (x - y) but sometimes the number of squares associated with a color is 3 and sometimes its 4 (sometimes it's also 2 but I could figure those out).

Just shells for 5, 7, 9, 11 for which diagonals are easily available

What is the best way to describe these shells so as to be able to translate coordinates to their appropriate shell?

Campbell Hutcheson
  • 205
  • @ParclyTaxel I'm trying to answer the question in a specific way by finding an equation to describe the octagons. That said, any answer must describe the octagons so that probably describes them! So, thank you for point me to that resource! – Campbell Hutcheson Aug 10 '22 at 15:51
  • You can "fold" the coordinates along the diagonals, such that all the coordinates are in the triangle between $(0,0),(0,x)$, and $(x,x)$. It's not $C_8$ symmetry, but $C_{4d}$, so giving one point $(a,b)$ implies the points $(\pm a, \pm b)$ and $(\pm b, \pm b)$. The only exception is when $a=b$ or either coordinate is $0$; note that the former only happens for even numbers of moves. – Eric Snyder Aug 11 '22 at 09:10
  • Or rather than defining individual points, we can be even simpler. For $k=5$, all valid points have $x+y$ odd, within the bounds $7 \le x \le 10, x+y \le 15$, and the other seven trapezoids generated by reflection and rotation. In general for odd $k \ge 5$, you have $x+y$ odd, $k+2 \le x \le k+5, x+y \le 8k+7$. (Note: the trapezoids overlap.) – Eric Snyder Aug 11 '22 at 09:43
  • (Darn, that misses a couple of points and would need some refining. But I think you get the gist. – Eric Snyder Aug 11 '22 at 09:48

0 Answers0