Determining an ellipse inscribed in a rectangle given its tangent point at one of the sides

Question

Given a rectangle $PQRS$ with vertices $P(0,0), Q(a, 0), R(a,b), S(0, b)$ I want to determine the equation of the ellipse inscribed in it, and touching it bottom edge at $T(c, 0)$ where $0 \lt c \lt a $.

My attempt is summarized as follows: First, from symmetry of the ellipse with respect to the rectangle, then the center of the ellipse will be at $C = \dfrac{1}{2} (a, b ) $. Second, using matrix-vector notation, let $ p = [x,y ]^T $ be a point on this inscribed ellipse, then $p$ satisfies the ellipse equation which is

$ (p - C)^T A (p - C) = 1 \hspace{12pt}(1) $

for some symmetric positive definite $2 \times 2 $ matrix $A$. Since $A$ is symmetric, it is determined by three scalars which are $A_{11}, A_{12}, A_{22} $

Since the point $T (c, 0)$ is on the ellipse then

$ (T - C)^T A (T - C) = 1 \hspace{12pt} (2)$

Tangency to the bottom side, tells us that the gradient of the ellipse (which points in the outward normal vector direction) is along the $-j$ vector, where $j$ is the unit vector in the positive $y$ axis direction.

Therefore, let's first compute the gradient. It is given by

$ g(p) = 2 A (p - C) \hspace{12pt} (3)$

From the above, we have

$ A(T - C) = - \alpha j $, for some $\alpha \gt 0 \hspace{12pt}(4) $

From this last equation it follows that

$ T - C = - \alpha A^{-1} j \hspace{12pt}(5) $

Substituting this into the equation of the ellipse, we find that $\alpha$ is given by

$ \alpha = \dfrac{1}{\sqrt{j^T A^{-1} j}} \hspace{12pt}(6) $

Pre-multiplying both sides of equation $(5)$ by $j^T$ , we get

$ j^T (T - C) = 0 - \dfrac{b}{2} = - \dfrac{ j^T A^{-1} j }{ \sqrt{ j^T A^{-1} j } } = - \sqrt{j^T A^{-1} j } \hspace{12pt} (7) $

Now, $j^T A^{-1} j = {A^{-1}}_{(22)} \hspace{12pt} (8) $

Now I am stuck in trying to find the elements $A_{11}, A_{12}, A_{22} $.

Equation (2) gives one linear equation in these three unknowns. Taking the first component of Equation (4) gives another linear equation in $A_{11}$, and $A_{12} $. Equations (7),(8) state that

$ (A^{-1})_{22} = \bigg(\dfrac{b}{2}\bigg)^2 \hspace{12pt}(9) $

which is basically saying that

$ \dfrac{ A_{11}}{A_{11}A_{22} - A_{12}^2 } = \bigg(\dfrac{b}{2}\bigg)^2 $

But how can I solve these three equations? That's where I am stuck.

Your help is greatly appreciated.

EDIT:

Thanks to a comment by @Ethan Bolker, I've realised that that, in the above, I did not use any information about the width of the rectangle, i.e. the input parameter $a$. So we have to somehow find the tangency point of the inscribed ellipse with the left or right side. Since the given rectangle is an affine transformation of a square (a dilation in the $x$ and $y$) and since by inspection of an ellipse inscribed in a square, it is clear (without proof) that the ratio the bottom tangent point distance from the left bottom corner to the width $a$ is the same as the ratio as the left tangent point of the inscribed ellipse distance from the left bottom corner to the height $b$. Thus if the left tangent point if $L(0, d)$ then

$ \dfrac{d}{b} = \dfrac{c}{a} \hspace{12pt}(10)$

Now apply the same logic in the above analysis, we deduce that

$ L - C = - \beta A^{-1} i \hspace{12pt} (11)$

where $i$ is the unit vector along the positive $x$ axis. And using the same reasoning as above, we deduce that

$ \beta = \dfrac{1}{\sqrt{ i^T A^{-1} i }} \hspace{12pt}(12)$

Pre-multiplying $(11)$ with $i^T$

$ i^T (L - C) = 0 - \dfrac{a}{2} = - \sqrt{i^T A^{-1} i } \hspace{12pt}(13) $

Now, using either $(5)$ or $(11)$, we have an equation isolating $A^{-1}_{(12)} $

Using $(5)$,

$i^T (T - C) = c - \dfrac{a}{2} = - \dfrac{i^T A^{-1} j }{\sqrt{j^T A^{-1} j }} \hspace{12pt}(14) $

And alternatively, using $(11)$

$ j^T (L - C) = \dfrac{bc}{a} - \dfrac{b}{2} = - \dfrac{ j^T A^{-1} i }{\sqrt{i^T A^{-1} i}} \hspace{12pt}(15)$

We can now use equations $(9)$ , we can solve immediately for $A^{-1}_{(22)} $, and from $(13)$ we find $A^{-1}_{(11)} $, and finally, using either $(14)$ or $(15)$ we can find $A^{-1}_{(12)} $.

That is,

$ A^{-1}_{(22)} =\bigg(\dfrac{b}{2}\bigg)^2 \hspace{12pt}(16) $

$ A^{-1}_{(11)} =\bigg(\dfrac{a}{2}\bigg)^2 \hspace{12pt}(17) $

$ A^{-1}_{(12)} =- \bigg(c - \dfrac{a}{2}\bigg) \dfrac{b}{2} \hspace{12pt}(18) $

Now $A^{-1}$ is determined, therefore $A$ is determined.

I appreciate any alternative methods to determine the ellipse.

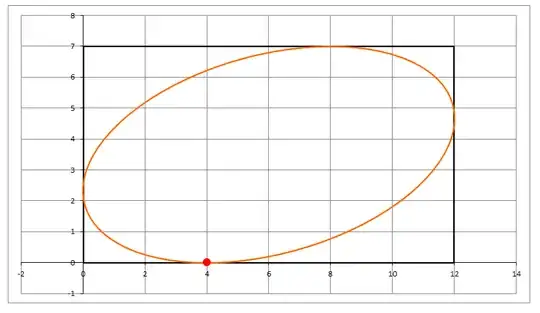
UPDATE: I applied the above method to a rectangle with $a = 12, b = 7$ and $c = 4$ and got the ellipse shown in the figure below

Answer 1

Partial solution in response to a comment.

Inscribe an ellipse in the square with vertices $(\pm 1, 0), (0, \pm 1)$. The ellipse will have equation $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ and the slope will be given by $$ \frac{2xdx}{a^2} + \frac{2ydy}{b^2} = 0. $$

We want the ellipse that goes through the point $(s,t)$ where $s+t = 1$ and to have slope $dy = -dx$ at that point.

Therefore $$ \frac{s^2}{a^2} + \frac{t^2}{b^2} = 1 $$ and $$ \frac{s}{a^2} - \frac{t}{b^2} = 0. $$ You can solve the second of these equations together with $s+t=1$ to find a relation between $a^2$ and $b^2$ to use along with the first equation to find $a^2$ and $b^2$.

Answer 2

First method.

We know the equation must be of the form $$ \alpha(x-x_C)^2+\beta(x-x_C)(y-y_C)+\gamma(y-y_C)^2=1, $$ where $C=(a/2,b/2)$ is the centre. We already know the coordinates of two points of the ellipse: $$ T=(c,0),\quad L=(0,bc/a), $$ we need another one to find coefficients $\alpha$, $\beta$, $\gamma$. It's easy to find the coordinates of point $D$, which is an intersection between diagonal $PR$ and the ellipse (see figure below), because: $$ CP:CD=CD:CM, $$ where $M=\big(c/2,bc/(2a)\big)$ is the midpoint of $TL$. This property is easily verified for a circle, and is still valid for an ellipse, because stretching preserves ratios on a line. We thus get: $$ D=\left({1-\sqrt{1-c/a}\over2}a, {1-\sqrt{1-c/a}\over2}b \right). $$ Plugging the coordinates of $T$, $L$ and $D$ into the equation, we can solve for $\alpha$, $\beta$ and $\gamma$.

Second Method.

If $U$ is an intersection of the ellipse with a line through $C$, parallel to $PQ$, then $CU$ is a semi-diameter conjugated with $CT$. Length $CU$ can be found from another property of conjugate diameters:

$$ \left({LH\over CU}\right)^2+\left({CH\over CT}\right)^2=1, $$ where $H$ is on $CT$ and $LH\parallel PQ$.

From that, one can find the coordinates of $U$ and write a parametric equation for a generic point $A(t)$ on the ellipse: $$ A(t)=C+(U-C)\cos t+(T-C)\sin t. $$