Get the position by only knowing a landmark and the relative position to it

Question

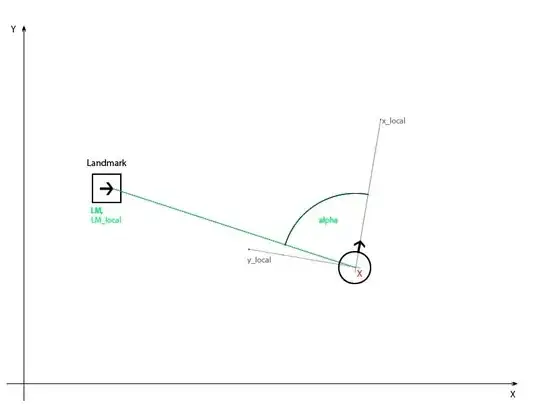
I have a little problem finding a solution for this problem:

My position is unknown. I can see a landmark (angle, range) and so I know the position $LM_{local}$ in my local coordinate frame.
I recognized this landmark, and so I also know the global position of this landmark. LM(x,y, $\theta$)

But I have a problem finding my global position.
I only get a correct position at a specific orientation of myself. When I turn myself in place, the calculated position goes in a circle around the landmark...

I think my problem could be, not knowing the orientation of the landmark in my local coordinate system... But I am not sure...

Is this problem solvable with one landmark?

The green elements are known, and the red X is the position to be calculated.
enter image description here

Ron Gordon · Accepted Answer · 2013-07-22T20:53:42.527

1

In vector notation, you know the vector of the landmark $\vec{L}$ with respect to some origin $O$, and the position of the landmark relative to unknown position $\vec{R}$. The unknown position $\vec{P}$ with respect to $O$ is simply

$$\vec{P}=\vec{L}-\vec{R}$$

The vector subtraction means that, when a vector is expressed in terms of Cartesian coordinates, you subtract each component.

EDIT

I may have oversimplified this. Basically, I think you know a position of a landmark with respect to both a local and global origin, and you know how you are oriented. You just do not know where you are with respect to the global origin.

The relationship between the local and global coordinate system is as follows:

$$x'=x_0+x \cos{\theta}-y \sin{\theta}$$ $$y'=y_0+x \sin{\theta}+y \cos{\theta}$$

where $(x_0,y_0)$ is the unknown location of the local origin in the global coordinate system, $(x,y)$ is the location of the landmark in the global coordinate system, $(x',y')$ is the position of the landmark in the local coordinate system, and $\theta$ is your orientation angle. Knowing your data, it is straightforward to find your position.

edited Jul 22 '13 at 20:53

answered Jul 22 '13 at 19:23

Ron Gordon

141,538

Yes, but I get the relative position of the LM by converting from polar to Cartesian coordinates. x = length * cos (angle), so when I turn myself, the angle changes, and so does the relative position. Goes around the landmark in a circle. – madmax Jul 22 '13 at 19:43
@madmax: if you are going to change your coordinate system, then the relative position changes, sure. The relationship I stated, however, is immutable. – Ron Gordon Jul 22 '13 at 20:09
So, the problem is not solvable? Because the x-axes is the direction of my position and so changes by turning? – madmax Jul 22 '13 at 20:34
@madmax: see my edit above. – Ron Gordon Jul 22 '13 at 20:53
@RonGordon I hope you enjoy this – Pedro Jul 23 '13 at 01:36
@PeterTamaroff: indeed! – Ron Gordon Jul 23 '13 at 01:48
@RonGordon I'm glad! – Pedro Jul 23 '13 at 01:55

Get the position by only knowing a landmark and the relative position to it

1 Answers1