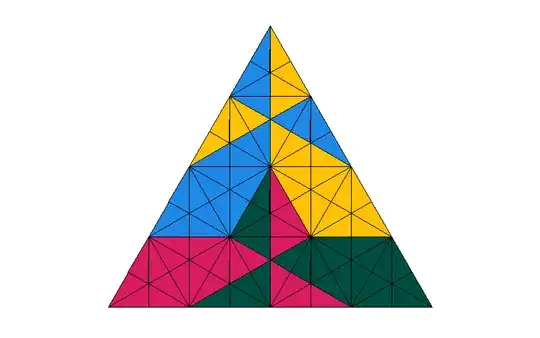
Suppose we wish to divide an equilateral triangle into fourths, such that each piece is congruent. (Let's also require connectedness.) One way to do this is to connect the medians, forming one inverted triangle in the center and three at the corners. Is this the only way? Are there any other ways to divide an equilateral triangle into congruent fourths?
Asked
Active
Viewed 287 times
10
-
Take three line segments from one vertex to the opposite edge. – John Douma Jul 12 '22 at 16:21
-
2@JohnDouma Those won't be congruent. – Akiva Weinberger Jul 12 '22 at 16:22
-
You can deform the common sides between two triangles in such a way to keep them congruent. – Intelligenti pauca Jul 12 '22 at 16:39
-
@Intelligentipauca The issue is, if you're starting from the connect-the-medians solution, you can't get two disjoint pairs of adjacent triangles. – Akiva Weinberger Jul 12 '22 at 16:45
-
@AkivaWeinberger You're right, that won't work. – Intelligenti pauca Jul 12 '22 at 16:47
-
I think you mean 'the midpoints of the sides", not "the medians". A median is usually a line connecting a vertex to the midpoint of the opposite side. – MJD Oct 19 '22 at 22:26
1 Answers
8
Depending on how strict you are with your notion of connectedness, here are four congruent sets whose closures are connected and whose interiors are disjoint:
RavenclawPrefect
- 18,328
-
Nice! But: if these shapes are all taken to contain the point at which the three pieces meet (which is not possible since that point is the same point for red + green, and for yellow + orange) then they are contractible; otherwise, they are disconnected. Either way, where is the nontrivial $\pi_1$? – Qiaochu Yuan Oct 19 '22 at 21:16
-
Good point - sloppy wording on my part, I'll edit. Do you know of nice terminology for the notion of not-quite-connectedness that applies here? – RavenclawPrefect Oct 19 '22 at 22:12
-
1Well, the point is called a cut point (https://en.wikipedia.org/wiki/Cut_point). I don't know if there's any name in particular for a space with a cut point. – Qiaochu Yuan Oct 19 '22 at 22:14
-
Cool! That's a pretty unexpected configuration. How did you find it? – Akiva Weinberger Oct 20 '22 at 19:25
-
I was inspired by this decomposition of an equilateral triangle into 5 pieces, and realized that the problem of writing a union of finitely many congruent cells as a collection of subsets related to each other by one of a finite set of isometries could be expressed as a not-too-large SAT instance; I wrote some code to generate such instances, and then plugged it into an off-the-shelf solver in Python. One of the solutions had remarkably few edge-connected components in each piece (compared to e.g. this). – RavenclawPrefect Oct 20 '22 at 19:30
-
1Of course, this still leaves open the question of a strongly connected decomposition. (Call a piece weakly connected if the closure of its interior is connected, and strongly connected if its interior is connected; I think that captures the idea well enough.) I strongly suspect this is impossible, which will require an impossibility proof – Akiva Weinberger Oct 20 '22 at 19:58