7

Let $\mathcal{A}$ be an abelian category. Given a commutative square $$ \require{AMScd} \begin{CD} A@>f>>B\\ @VVV@VVV\\ A'@>>{f'}>B' \end{CD} $$ in $\mathcal{A}$, we get an induced morphism between kernels $\operatorname{Ker}f\to\operatorname{Ker}f'$, namely, the unique one that makes the diagram $$ \require{AMScd} \begin{CD} \operatorname{Ker} f@>>>A\\ @VVV@VVV\\ \operatorname{Ker}f'@>>{}>A' \end{CD} $$ commutative. I was trying to prove the following

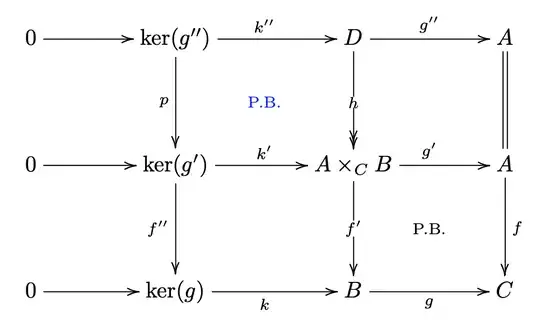
Lemma. Let $$ \require{AMScd} \begin{CD} A\times_CB@>{p}>>A\\ @V{q}VV@VV{f}V\\ B@>>{g}>C \end{CD} $$ be a cartesian square in $\mathcal{A}$. If $h:D\twoheadrightarrow A\times_CB$ is a surjection, then the induced morphism between kernels from the commutative square $$ \require{AMScd} \begin{CD} D@>>>A\\ @VVV@VV{f}V\\ B@>>{g}>C \end{CD} $$ is also surjective.

For me “surjective morphism” in an abelian category means an epimorphism or a morphism with zero cokernel (these two conditions are equivalent).

The proof is easily done in $\mathcal{A}=R\operatorname{-Mod}$ the category of left $R$-modules: if $b\in B$ is such that $g(b)=0$, then $(0,b)\in A\times_CB$, and there is $d\in D$ such that $h(d)=(0,b)$. Thus $d\in\operatorname{Ker}(D\to A)$. Also, in particular $d$ maps to $b$ in $B$. How one would do the proof in general? Is it okay to invoke Mitchell's embedding theorem or is it an overkill because there is an easier way? I don't exactly know how to translate the preceding element-wise diagram-chasing to a morphism-wise chasing using universal properties.

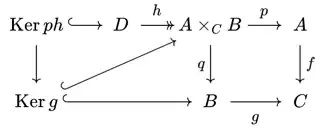
Edit: Okay this is what I've come up with so far. Using the universal property of the fibre product, there exists a morphism $\operatorname{Ker}g\to A\times_C B$ such that in the diagram

enter image description here

the composite $\operatorname{Ker}g\to A\times_CB\xrightarrow{q} B$ equals $\operatorname{Ker}g\to B$ and the composite $\operatorname{Ker}g\to A\times_CB\xrightarrow{p}A$ vanishes. Moreover, the morphism $\operatorname{Ker}g\to A\times_CB$ has to injective since after post-composition with $q$ we get an injective morphism $\operatorname{Ker}g\to B$. Also we have that the top left triangle of the diagram commutes, since equality of the two sides of the triangle can be verified after post-composition with $p$ and $q$.

But now I don't know how to continue. I haven't used the surjectivity of $h$ yet, and I don't know how to use it exactly.

For those who may ask why am I interested on this result: I'm trying to understand the proof of 05T7 of the Stacks Project. The proof is done by induction, and the verification of the induction hypothesis $IH_{n-1}$, which “the reader easily checks,” require to verify that an induced morphism between kernels is surjective. The above lemma abstracts the situation from the proof.

I know that there are posts here on MSE that address the same result I've linked from the Stacks Project, like this one. However, this last post uses other strategy, and I was interested on understanding the one from the SP.

Elías Guisado Villalgordo
  • 4,758

1 Answers1

2

Edit: the answer is essentially the same, but I simplified it a little, added details, and a new picture. I have also slightly changed my notations to better adapt them to yours.

Consider the following commutative diagram with exact rows, where the lower right square is your pullback and $h$ is your epimorphism:

enter image description here

In the notation of the above picture, you are asking to prove that the composition $f''\circ p$ is an epimorphism. Of course, it is enough to show that both $f''$ and $p$ are epimorphisms:

  • $f''$ is an epimorphism: note that the maps $k\colon \ker(g)\to B$ and $0\colon \ker(g)\to A$ are such that $g\circ k=0=f\circ 0$ so that, by the universal property of the pullback, there is a unique morphism $\bar k\colon \ker(g)\to A\times_CB$ such that $f'\circ \bar k=k$ and $g'\circ \bar k=0$. The latter condition tells us that, by the universal property of the kernel, there is a unique morphism $\tilde k\colon \ker(g)\to \ker(g')$ such that $k'\circ\tilde k=\bar k$. Then, $$k\circ f''\circ \tilde k=f'\circ k'\circ \tilde k=f'\circ \bar k=k=k\circ \mathrm{id}_{\ker(g)},$$ which shows that $f''\circ \tilde k=\mathrm{id}_{\ker(g)}$ since $k$ is a monomorphism. In particular, $f''$ is an epimorphism. (In fact, $f''$ is an isomorphism, see The Stacks project, Tag: 08N3, with inverse $\tilde k$, but this is not needed here).

  • $p$ is an epimorphism: just note that $\ker(g'')=h^{-1}(\ker(g'))$, that is, the upper left square is also a pullback, and epimorphisms are pullback stable (see, e.g., The Stacks project, Tag: 08N4).

Simone
  • 2,044
  • In case you haven't seen it: shortly before you posted your answer, I added an edit where I did the same thing as you did on your second paragraph – Elías Guisado Villalgordo Jun 23 '22 at 16:09
  • Yes, I saw it after posting. The moral is the following: your argument (=the argument in the second paragraph of the answer) proves the lemma for the epimorphism $id_{A\times_CB}\colon A\times_CB\to A\times_CB$, that is, the induced map $\ker(g')\to \ker(g)$ is epic. Now, as any other epimorphism $p\colon P\to A\times_CB$ factors through $id_{A\times_CB}$, you have that the kernel of $g'\circ p$ always maps onto $\ker(g')$, which maps onto $\ker(g)$ by the first part. – Simone Jun 23 '22 at 16:14
  • If you need more details, just let me know and I will edit the answer with the required explanations! – Simone Jun 23 '22 at 16:17
  • Thanks! You're using 08N4, right? – Elías Guisado Villalgordo Jun 23 '22 at 16:27
  • I am not sure about your reference. In less sketchy terms, the argument is the following: let $k\colon \ker(g)\to B$ and $k''\colon \ker(g')\to A\times_CB$ be the inclusions. The canonical morphism $f''\colon \ker(g')\to \ker(g)$ is then the unique such that $k\circ f''=f'\circ k'$. In particular, $f''$ is epic if and only if $\ker(g)\leq \mathrm{Im}(f')$. In the second paragraph of the answer I show exactly that $\ker(g)=f'(0\times_C\ker(g))\leq \mathrm{Im}(f')$, so $f''\colon \ker(g')\to \ker(g)$ is epic. – Simone Jun 23 '22 at 16:35
  • To conclude, let now $p\colon P\to A\times_CB$ be an epimorphism and $k''\colon \ker(g'\circ p)\to P$ be the inclusion of the kernel. Then, $f'''\colon \ker(g'\circ p)\to \ker(g)$ is the unique map such that $k\circ f'''=(p\circ f')\circ k''$. You can prove easily that $\mathrm{Im}(f''')=f'''(\ker(g'\circ p))\leq f''(\ker(g'))=\ker(g)$, so $f'''$ is also epic. – Simone Jun 23 '22 at 16:43
  • You can certainly add your answer or, if you prefer, you can edit mine, and I will then correct it if I see any mistake. – Simone Jun 23 '22 at 16:44
  • 1
    Sorry, now I see what you meant by "using 08N4"! Yes, that gives you that $p_{\restriction p^{-1}(0\times_C\ker(g))}$ is epic. – Simone Jun 23 '22 at 16:52