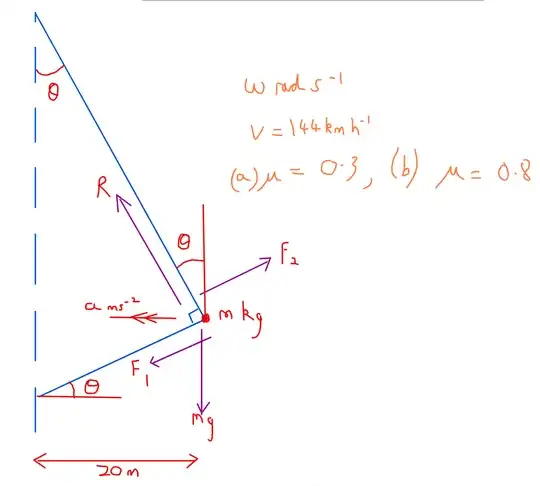
I came up with this question, to try to help my understanding with uniform circular motion of an object on a banked slope:
A car moving with speed $144$kmh$^{-1}$ is on a banked inward slope, the slope has angle $\theta^{\circ}$ to the horizontal. The car moves in a circular horizontal path of radius $20$m. Find the range of values of $\theta$ so that the car doesn't slip up or down the slope when the coefficient of friction between the car and the slope is $\ (a)\ 0.3\quad (b)\ 0.8.$
My attempt:
Speed = $v=\frac{144}{3.6} = 40$ms$^{-1}.\quad a=\frac{v^2}{r}=\frac{40^2}{20} = 80$ms$^{-2}.$
$(a)$ When the car is about to slip outwards, Friction = $F_1 = 0.3R.$ Resolving vertically upwards, $\ (F=ma):\ R\cos\theta-F_1\sin\theta =mg,\implies R(\cos\theta - 0.3\sin\theta) = mg\quad (1).$
Resolving horizontally towards the centre of the circle, $\ (F=ma):\ R\sin\theta + F_1\cos\theta = 80m, \implies r(\sin\theta + 0.3\cos\theta) = 80m.\quad (2)$
$$\frac{(2)}{(1)}:\ \frac{\sin\theta + 0.3\cos\theta}{\cos\theta - 0.3\sin\theta} = \frac{80}{9.8},\implies \left( 1 + \frac{24}{9.8} \right) \sin\theta = \left( \frac{80}{9.8} - 0.3 \right) \cos\theta, $$
$$\implies \tan\theta = 2.28 \implies \theta_{\min} = 66.3^{\circ.}$$
$$$$
When the car is about to slip inwards, Friction = $F_2 = 0.3R.$ Resolving vertically upwards, $\ (F=ma):\ R\cos\theta+F_2\sin\theta =80m,\implies R(\cos\theta + 0.3\sin\theta) = mg\quad (3).$
Resolving horizontally towards the centre of the circle, $\ (F=ma):\ R\sin\theta - F_2\cos\theta = 80m, \implies r(\sin\theta - 0.3\cos\theta) = 80m.\quad (4)$
$$\frac{(3)}{(4)}:\ \frac{\sin\theta - 0.3\cos\theta}{\cos\theta + 0.3\sin\theta} = \frac{80}{9.8} \implies \left( 1 - \frac{24}{9.8} \right) \sin\theta = \left( \frac{80}{9.8} + 0.3 \right) \cos\theta $$
$$\implies \tan\theta = -5.84 \implies \theta_{\max} = -80.3^{\circ.}$$
But having negative degrees here means something is wrong with my working or thought process.
Also, I tried the same calculations with $0.3$ replaced with $0.8$ for $(b),$ and got $ 44^{\circ}< \theta < 58.3^{\circ},$ but I thought $\theta_{\max}$ should be greater than $58.3^{\circ}.$
So what is going on here?